题目内容
11.已知△ABC中,tanB=$\frac{2}{3}$,BC=6,过点A作BC边上的高,垂足为点D,且满足BD:CD=2:1,则△ABC面积的所有可能值为8或24.分析 分两种情况,根据已知条件确定高AD的长,然后根据三角形面积公式即可求得.
解答 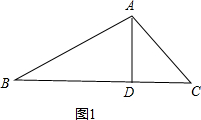 解:如图1所示:
解:如图1所示:
∵BC=6,BD:CD=2:1,
∴BD=4,
∵AD⊥BC,tanB=$\frac{2}{3}$,
∴$\frac{AD}{BD}$=$\frac{2}{3}$,
∴AD=$\frac{2}{3}$BD=$\frac{8}{3}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×$\frac{8}{3}$=8;
如图2所示: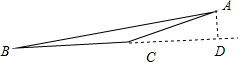 ∵BC=6,BD:CD=2:1,
∵BC=6,BD:CD=2:1,
∴BD=12,
∵AD⊥BC,tanB=$\frac{2}{3}$,
∴$\frac{AD}{BD}$=$\frac{2}{3}$,
∴AD=$\frac{2}{3}$BD=8,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×8=24;
综上,△ABC面积的所有可能值为8或24,
故答案为8或24.
点评 本题考查了解直角三角形,以及三角函数的定义,三角形面积,分类讨论思想的运用是本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
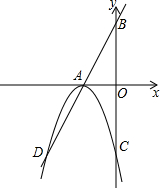 如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,
如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,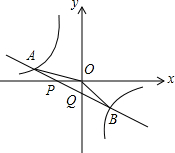 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.