题目内容
20.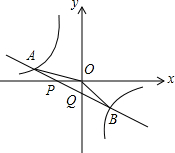 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.
分析 根据一次函数和反比例函数的性质得到k1k2>0,故①错误;把A(-2,m)、B(1,n)代入y=$\frac{{k}_{2}}{x}$中得到-2m=n故②正确;把A(-2,m)、B(1,n)代入y=k1x+b得到y=-mx+m,求得P(-1,0),Q(0,-m),根据三角形的面积公式即可得到S△AOP=S△BOQ;故③正确;根据图象得到不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,故④正确.
解答 解:由图象知,k1<0,k2<0,
∴k1k2>0,故①错误;
把A(-2,m)、B(1,n)代入y=$\frac{{k}_{2}}{x}$中得-2m=n,
∴m+$\frac{1}{2}$n=0,故②正确;
把A(-2,m)、B(1,n)代入y=k1x+b得$\left\{\begin{array}{l}{m=-2{k}_{1}+b}\\{n={k}_{1}+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{1}=\frac{n-m}{3}}\\{b=\frac{2n+m}{3}}\end{array}\right.$,
∵-2m=n,
∴y=-mx-m,
∵已知直线y=k1x+b与x轴、y轴相交于P、Q两点,
∴P(-1,0),Q(0,-m),
∴OP=1,OQ=m,
∴S△AOP=$\frac{1}{2}$m,S△BOQ=$\frac{1}{2}$m,
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,故④正确;
故答案为:②③④.
点评 本题考查了反比例函数与一次函数的交点,求两直线的交点坐标,三角形面积的计算,正确的理解题意是解题的关键.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案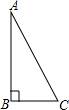 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:| 小钟作法: (1)作AC的垂直平分线MN,垂足为点O; (2)连接BO,并延长BO至点D,使DO=BO; (3)连接AD,CD 所以,四边形ABCD就是所要求作的矩形 |
| 小国作法: (1)分别以A,C为圆心,以BC,AB为半径作弧,两弧交于点D; (2)连接AD,CD. 所以,四边形ABCD就是所要求作的矩形. |
| A. | 小钟的作法正确 | B. | 小国的作法正确 | ||
| C. | 小钟和小国的作法都正确 | D. | 赞同小孟的观点 |
| A. |  | B. |  | C. |  | D. |  |
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
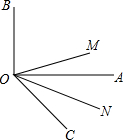 如图,ON平分∠AOC,OM平分∠BOC.
如图,ON平分∠AOC,OM平分∠BOC.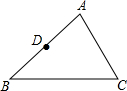 如图,已知△ABC中,D为AB的中点.
如图,已知△ABC中,D为AB的中点.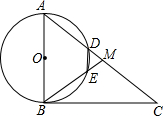 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.