题目内容
16.已知关于x的方程$\frac{2}{x}$=m的解满足$\left\{\begin{array}{l}{x-y=3-n}\\{x+2y=5n}\end{array}\right.$(0<n<3),若y>1,则m的取值范围是$\frac{2}{5}$<m<$\frac{2}{3}$.分析 先解方程组$\left\{\begin{array}{l}{x-y=3-n}\\{x+2y=5n}\end{array}\right.$,求得x和y,再根据y>1和0<n<3,求得x的取值范围,最后根据$\frac{2}{x}$=m,求得m的取值范围.
解答 解:解方程组$\left\{\begin{array}{l}{x-y=3-n}\\{x+2y=5n}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=n+2}\\{y=2n-1}\end{array}\right.$
∵y>1
∴2n-1>1,即n>1
又∵0<n<3
∴1<n<3
∵n=x-2
∴1<x-2<3,即3<x<5
∴$\frac{1}{5}$<$\frac{1}{x}$<$\frac{1}{3}$
∴$\frac{2}{5}$<$\frac{2}{x}$<$\frac{2}{3}$
又∵$\frac{2}{x}$=m
∴$\frac{2}{5}$<m<$\frac{2}{3}$
故答案为:$\frac{2}{5}$<m<$\frac{2}{3}$
点评 本题主要考查了分式方程的解以及二元一次方程组的解,解题时需要掌握解二元一次方程和一元一次不等式的方法.根据x取值范围得到$\frac{1}{x}$的取值范围是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
4.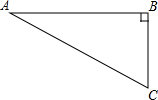 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.函数y=$\frac{2}{x+1}$的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
6.点P(-2,-3)向右平移2个单位,再向下平移3个单位,则所得到的点的坐标为( )
| A. | (0,0) | B. | (-4,0) | C. | (0,-6) | D. | (0,6) |
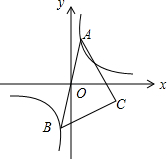 如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.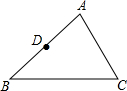 如图,已知△ABC中,D为AB的中点.
如图,已知△ABC中,D为AB的中点.