题目内容
3.已知点P(a,b)是反比例函数y=$\frac{1}{x}$的图象上异于点(-1,-1)的一个动点,则$\frac{1}{1+a}+\frac{1}{1+b}$=1.分析 利用反比例函数图象上点的坐标性质得出ab=1,再利用分式的混合运算法则求出即可.
解答 解:∵P(a,b)是反比例函数y=$\frac{1}{x}$的图象上异于点(-1,-1)的一个动点,
∴ab=1,
∴$\frac{1}{1+a}+\frac{1}{1+b}$=$\frac{1+b}{(1+a)(1+b)}$+$\frac{1+a}{(1+a)(1+b)}$=$\frac{2+a+b}{1+a+b+ab}$=$\frac{2+a+b}{2+a+b}$=1.
故答案为1.
点评 此题主要考查了反比例函数图象上点的坐标性质以及分式的混合运算,正确化简分式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.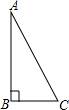 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
小孟说:“他们的作法都错误.”你的观点是( )
 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:| 小钟作法: (1)作AC的垂直平分线MN,垂足为点O; (2)连接BO,并延长BO至点D,使DO=BO; (3)连接AD,CD 所以,四边形ABCD就是所要求作的矩形 |
| 小国作法: (1)分别以A,C为圆心,以BC,AB为半径作弧,两弧交于点D; (2)连接AD,CD. 所以,四边形ABCD就是所要求作的矩形. |
| A. | 小钟的作法正确 | B. | 小国的作法正确 | ||
| C. | 小钟和小国的作法都正确 | D. | 赞同小孟的观点 |
12.东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
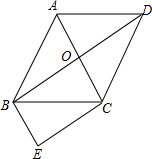 如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
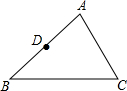 如图,已知△ABC中,D为AB的中点.
如图,已知△ABC中,D为AB的中点. 如图,△OAB绕点O逆时针旋转90°到△OCD的位置,已知∠AOB=40°,则∠AOD的度数为50°.
如图,△OAB绕点O逆时针旋转90°到△OCD的位置,已知∠AOB=40°,则∠AOD的度数为50°.