题目内容
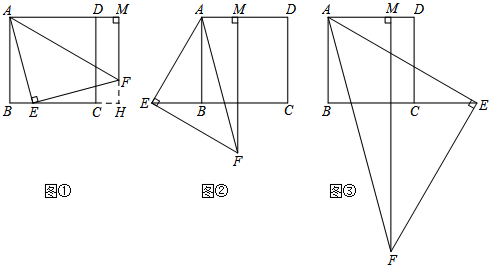
2.已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.(1)当点E在边BC上,点M在边AD的延长线上时,如图①,请直接写出线段AB,BE,AM之间的数量关系:AB+BE=AM;
(2)当点E在边CB的延长线上,点M在边AD上时,如图②;请探索线段AB,BE,AM之间的数量关系,并证明;
(3)若BE=$\sqrt{6}$,∠AFM=15°,则AM=3$\sqrt{2}$-$\sqrt{6}$或$\sqrt{6}$-$\sqrt{2}$.
分析 (1)首先利用等腰直角三角形的性质和正方形的性质得AE=EF,∠ABE=∠EHF=90°,利用全等三角形的判定定理证明△ABE≌△EHF,再利用全等三角形的性质定理可得结论;
(2)同(1)首先证明△ABE≌△EHF,再利用全等三角形的性质定理可得结论;
(3)利用分类讨论的思想,首先由∠AFM=15°,易得∠EFH,由△ABE≌△EHF,根据全等三角形的性质易得∠AEB,利用锐角三角函数易得AB,利用(1)(2)的结论,易得AM.
解答  (1)证明:如图①,延长MF,交边BC的延长线于点H,
(1)证明:如图①,延长MF,交边BC的延长线于点H,
∵四边形ABCD是正方形,FM⊥AD,
∴∠ABE=90°,∠EHF=90°,四边形ABHM为矩形,
∴AM=BH=BE+EH
∵△AEF为等腰直角三角形,
∴AE=AF,∠AEB+∠FEH=90°,
∵∠EFH+∠FEH=90°,
∴∠AEB=∠EFH,
在△ABE与△EHF中,
$\left\{\begin{array}{l}{∠ABE=∠EHF=90°}\\{∠AEB=∠EFH}\\{AE=EF}\end{array}\right.$,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∵AM=BH=BE+EH,
∴AM=BE+AB,
即AB+BE=AM;
故答案为:AB+BE=AM;
(2)解:如图②,∵∠AEB+∠FEH=90°,∠AEB+∠EAB=90°,
∴∠FEH=∠EAB,
在△ABE与△EHF中,
$\left\{\begin{array}{l}{∠ABE=∠EHF}\\{∠EAB=∠FEH}\\{AE=FE}\end{array}\right.$,
∴△ABE≌△EHF(AAS),
∴AB=EH=EB+AM;
如图③∠BAE+∠AEB=90°,∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
在△ABE与△EHF中,
$\left\{\begin{array}{l}{∠ABE=∠EHF}\\{∠EAB=∠FEH}\\{AE=FE}\end{array}\right.$,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∴BE=BH+EH=AM+AB;
(3)解:如图①,∵∠AFM=15°,∠AFE=45°,
∴∠EFM=60°,
∴∠EFH=120°,
在△EFH中,
∵∠FHE=90°,∠EFH=120°,
∴此情况不存在;
如图②,∵∠AFM=15°,∠AFE=45°,
∴∠EFH=60°,
∵△ABE≌△EHF,
∴∠EAB=∠EFH=60°,
∵BE=$\sqrt{6}$,
∴AB=BE•tan60°=$\sqrt{6}$×$\sqrt{3}$=3$\sqrt{2}$,
∵AB=EB+AM,
∴AM=AB-EB=3$\sqrt{2}$-$\sqrt{6}$;
如图③,∵∠AFM=15°,∠AFE=45°,
∴∠EFH=45°-15°=30°,
∴∠AEB=30°,
∵BE=$\sqrt{6}$,
∴AB=BE•tan30°=$\sqrt{2}$,
∵BE=AM+AB,
AM=BE-AB=$\sqrt{6}$-$\sqrt{2}$,
故答案为:3$\sqrt{2}$-$\sqrt{6}$或$\sqrt{6}$-$\sqrt{2}$.
点评 本题主要考查了等腰直角三角形的性质,正方形的性质,全等三角形的性质及判定定理,数形结合,分类讨论,利用前面问题的结论是解答此题的关键.

| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
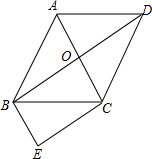 如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.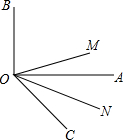 如图,ON平分∠AOC,OM平分∠BOC.
如图,ON平分∠AOC,OM平分∠BOC.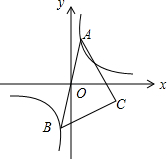 如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.