题目内容
6.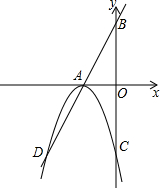 如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,
如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,(1)求抛物线解析式?
(2)将抛物线沿AB平移,此时顶点即为E,如顶点始终在AB上,平移后抛物线交y轴于F,求当△BEF于△BAO相似时,求E点坐标.
(3)记平移后抛物线与直线AB另一交点为G,则S△BFG与S△ACD是否存在8倍关系?若有,直接写出F点坐标.
分析 (1)易求得A、B的坐标,设出顶点式,代入C的坐标根据待定系数法即可求得解析式;
(2)由于顶点在直线AB上,根据题意设出解析式为y=-(x+2-m)2+2m,即可得出E(m-2,2m),F(0,-m2+6m-4),根据三角形相似的性质得出tan∠BFE=$\frac{2-m}{2m-(-{m}^{2}+6m-4)}$=2,解方程即可求得m的值,从而求得E的坐标;
(3)求得D的坐标,根据(2)可知G(-4+m,-4+2m),根据题意S△BFG=1或64,S△BFG=$\frac{1}{2}$BF•|xG|=$\frac{1}{2}$|4-(-m2+6m-4)|•|-4+m|,根据(2)中可知2m2-7m+6=0,则m2=3.5m-3 代入得S△BFG=$\frac{5}{4}$|m2-6m+8|,然后分两种情况列出关于m的方程,解方程求得m的值,即可求得F的坐标.
解答 解:(1)由直线AB解析式为y=2x+4可知A(-2,0),B(0,4),
∵A为抛物线顶点,
∴设顶点式y=a(x+2)2,
代入C(0,-4)得-4=4a,
解得a=-1,
∴抛物线解析式为y=-(x+2)2=-x2-4x-4;
(2)由于顶点在直线AB上,故可假设向右平移m个单位,再向上平移2m个单位、
即解析式为y=-(x+2-m)2+2m,
∴E(m-2,2m),F(0,-m2+6m-4),
∵△BAO∽△BFE,
∴tan∠BFE=tan∠BAO=2,
∵tan∠BFE=$\frac{2-m}{2m-(-{m}^{2}+6m-4)}$=2,
化简得2m2-7m+6=0,
解得m1=2(舍去,与B点重合),m2=$\frac{3}{2}$
∴E(-$\frac{1}{2}$,3);
(3)令2x+4=-x2-4x-4,解得D(-4,-4),
由于G点是由D点平移得来,在第二问的条件下,易得G(-4+m,-4+2m)
∴S△ACD=8,
∴S△BFG=1或64,
∵S△BFG=$\frac{1}{2}$BF•|xG|=$\frac{1}{2}$|4-(-m2+6m-4)|•|-4+m|,
由第二问可知,2m2-7m+6=0,则m2=3.5m-3 代入得S△BFG=$\frac{5}{4}$|m2-6m+8|,
①当$\frac{5}{4}$|m2-6m+8|=1时,
化简得m2-6m+8=±$\frac{4}{5}$,
∴-m2+6m=$\frac{44}{5}$或-m2+6m=$\frac{36}{5}$,
∵F(0,-m2+6m-4),
∴F1(0,$\frac{24}{5}$),F2(0,$\frac{16}{5}$);
②当$\frac{5}{4}$|m2-6m+8|=64时,
化简得m2-6m+8=±$\frac{256}{5}$,
∴-m2+6m=-$\frac{216}{5}$或-m2+6m=$\frac{296}{5}$(舍去,无解),
∵F(0,-m2+6m-4),
∴F3(0,-$\frac{236}{5}$),
综上,F点坐标为(0,$\frac{24}{5}$)或(0,$\frac{16}{5}$)或(0,-$\frac{236}{5}$).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,平移的性质,三角形相似的性质以及三角形的面积等,分类讨论思想的运用是解题的关键.

| A. | 36 | B. | 42 | C. | 45 | D. | 48 |
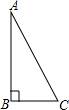 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:| 小钟作法: (1)作AC的垂直平分线MN,垂足为点O; (2)连接BO,并延长BO至点D,使DO=BO; (3)连接AD,CD 所以,四边形ABCD就是所要求作的矩形 |
| 小国作法: (1)分别以A,C为圆心,以BC,AB为半径作弧,两弧交于点D; (2)连接AD,CD. 所以,四边形ABCD就是所要求作的矩形. |
| A. | 小钟的作法正确 | B. | 小国的作法正确 | ||
| C. | 小钟和小国的作法都正确 | D. | 赞同小孟的观点 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
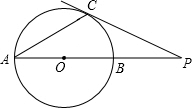 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为$\sqrt{3}$.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为$\sqrt{3}$.