题目内容
1.解方程:$\frac{x+5}{4}$=$\frac{2x-3}{6}$+2.分析 先去分母,然后通过移项、合并同类项,化系数为1进行解答即可.
解答 解:去分母,得3(x+5)=2(2x-3)+24.
整理,得3x+15=4x-6+24,
解得x=-3.
点评 本题考查了解一元一次方程.解一元一次方程常见的过程有去括号、移项、系数化为1等.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
12.东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
16.已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.点P(-2,-3)向右平移2个单位,再向下平移3个单位,则所得到的点的坐标为( )
| A. | (0,0) | B. | (-4,0) | C. | (0,-6) | D. | (0,6) |
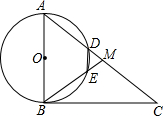 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E. 如图,△OAB绕点O逆时针旋转90°到△OCD的位置,已知∠AOB=40°,则∠AOD的度数为50°.
如图,△OAB绕点O逆时针旋转90°到△OCD的位置,已知∠AOB=40°,则∠AOD的度数为50°.