题目内容
8．分解因式：ab2+bc2+ca2+a2b+b2c+c2a+2abc．分析 首先利用拆项法将原式重新分组，进而利用提取公因式法分解因式即可．
解答 解：原式=（ab2+a2b+abc）+（bc2+b2c+abc）+（ca2+c2a）
=ab（a+b+c）+bc（a+b+c）+ac（a+c），
=（a+b+c）（ab+bc）+ac（a+c），
=b（a+b+c）（a+c）+ac（a+c），
=（a+c）[b（a+b+c）+ac]．
点评 此题主要考查了分组分解法分解因式，正确分组得出是解题关键．
练习册系列答案
习题精选系列答案
相关题目
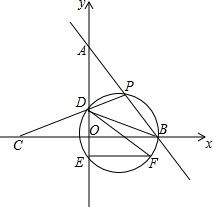如图，在平面直角坐标系中，O为坐标原点，直线y=-$\frac{4}{3}$x+4与x轴交于点B，与y轴交于点A，点C在x轴的负半轴上，并且OC=OB，一动点P在射线AB上运动，连结CP交y轴于点D，连结BD．过B，P，D三点作圆，交y轴与点E，过点E作EF∥x轴，交圆于点F，连结BF，DF．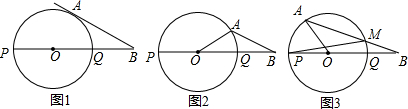
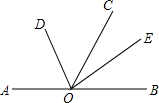16．已知5个正数，a，b，c，d，e的平均数是x，且a＜b＜c＜d＜e，则新一组数据a，b，0，c，d，e的平均数和中位数分别是（ ）
| A． | x，$\frac{c}{2}$ | B． | x，$\frac{b+c}{2}$ | C． | $\frac{5}{6}$x，$\frac{c}{2}$ | D． | $\frac{5}{6}x$，$\frac{b+c}{2}$ |
如图，直线AB上有点O，作射线OC，作OD平分∠AOC，OE平分∠BOC，求∠DOE的度数．
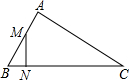如图，△ABC中，M是AB的中点，N在BC上，BC=2AB，∠BMN=∠C，则△BMN∽△BCA，相似比为$\frac{1}{4}$，$\frac{BN}{NC}$=$\frac{1}{7}$．