题目内容
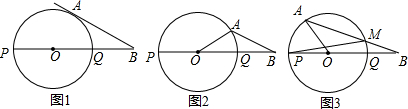
19.如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O上从点Q按逆时针方向运动到点P,连接AB,(1)当线段AB所在的直线与圆O相切时,求点A走过的路径(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
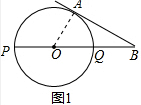
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求AB的长度(图3).
分析 (1)连接OA,根据直角三角形的性质求出∠B的度数,得到∠AOB的度数,根据弧长的计算公式求出点A走过的路径;
(2)根据直线与圆相切时,∠AOB的度数确定α的范围;
(3)连接MQ,根据三角形的中位线定理证明BM=MA,根据切割线定理求出AB的长.
解答 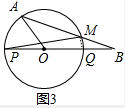
 解:(1)如图1,连接OA,
解:(1)如图1,连接OA,
∵直线AB与圆O相切,∴∠OAB=90°,又OA=$\frac{1}{2}$OB,
∴∠B=30°,则∠AOB=60°,
∴点A走过的路径为:$\frac{60π×1}{180}$=$\frac{π}{3}$;
(2)由(1)可知,当∠AOB=60°时,直线AB与圆O相切,
∴0°≤α≤60°;
(3)如图3,连接MQ,
∵PQ为圆O的直径,∴∠PMQ=90°,又AO⊥PM,
∴AO∥MQ,又BQ=OQ,
∴BM=MA,
由切割线定理,BM•BA=BQ•BP,
$\frac{1}{2}$AB2=1×3,
AB=$\sqrt{6}$.
点评 本题考查的是直线与圆相切、弧长的计算和切割线定理的应用,掌握弧长的计算公式和切割线定理是解题的关键.

练习册系列答案
相关题目
9.如图,在矩形ABCD中,AB<BC,AC,BD交于点O.点E为线段AC上的一个动点,连接DE,BE,过E作EF⊥BD于F,设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
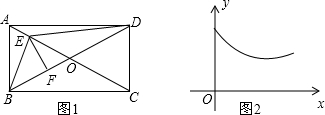

| A. | 线段EF | B. | 线段DE | C. | 线段CE | D. | 线段BE |
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )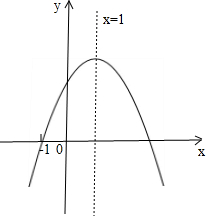

| A. | a>0 | B. | -1是方程ax2+bx+c=0的一个根 | ||
| C. | a+b+c=0 | D. | 当x<1时,y随x的增大而减小 |
11.下列事件是必然事件的是( )
| A. | 明天是晴天 | B. | 打开电视,正在播放动画片 | ||
| C. | 抛一枚硬币,正面朝上 | D. | 四边形的四个内角的和是360° |
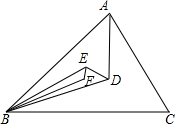 如图,D是△ABC的内心,E是△ABD的内心,F是△BDE的内心,若∠BFE的度数是整数,求∠BFE的最小度数.
如图,D是△ABC的内心,E是△ABD的内心,F是△BDE的内心,若∠BFE的度数是整数,求∠BFE的最小度数.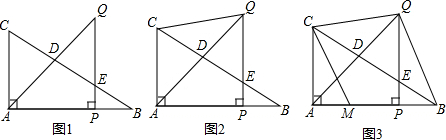
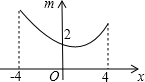
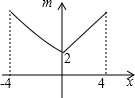
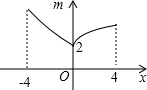
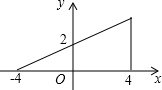 如图,若点P为函数y=kx+b(-4≤x≤4)图象上的一动点,m表示点P到原点O的距离,则下列图象中,能表示m与点P的横坐标x的函数关系的图象大致是( )
如图,若点P为函数y=kx+b(-4≤x≤4)图象上的一动点,m表示点P到原点O的距离,则下列图象中,能表示m与点P的横坐标x的函数关系的图象大致是( )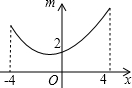
 如图,圆锥的高SO=4cm,底面圆的直径AB=6cm,求圆锥的侧面积.
如图,圆锥的高SO=4cm,底面圆的直径AB=6cm,求圆锥的侧面积.