题目内容
17.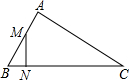 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
分析 根据∠BMN=∠C,∠B=∠B,推出△BMN∽△BCA,于是得到$\frac{BM}{BC}$=$\frac{BN}{AB}$=$\frac{1}{4}$,应用BC=2AB,得出BN=$\frac{1}{8}$BC,于是求得答案.
解答 解:∵M是AB的中点,
∴AB=2BM,
∵BC=2AB,
∴BC=4BM,
∵ ∠BMN=∠C,∠B=∠B,
∠BMN=∠C,∠B=∠B,
∴△BMN∽△BCA,
∴$\frac{BM}{BC}$=$\frac{BN}{AB}$=$\frac{1}{4}$,
∵BC=2AB,
∴BN=$\frac{1}{8}$BC,
∴$\frac{BN}{CN}$=$\frac{1}{7}$.
故答案为:BMN,BCA,$\frac{1}{4}$,$\frac{1}{7}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
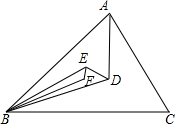 如图,D是△ABC的内心,E是△ABD的内心,F是△BDE的内心,若∠BFE的度数是整数,求∠BFE的最小度数.
如图,D是△ABC的内心,E是△ABD的内心,F是△BDE的内心,若∠BFE的度数是整数,求∠BFE的最小度数.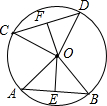 如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.
如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距. 如图,圆锥的高SO=4cm,底面圆的直径AB=6cm,求圆锥的侧面积.
如图,圆锥的高SO=4cm,底面圆的直径AB=6cm,求圆锥的侧面积.