题目内容
 在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.
在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.(1)求证:AM=BN;
(2)若AB=8,BC=6,求OM2+ON2的值.
考点:平行四边形的性质,勾股定理
专题:
分析:(1)由在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,易证得△ADM与△BCN是等腰三角形,继而证得结论;
(2)首先由在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,易求得△COD与△MON是直角三角形,然后由勾股定理求得OM2+ON2的值.
(2)首先由在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,易求得△COD与△MON是直角三角形,然后由勾股定理求得OM2+ON2的值.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,
∴∠CDM=∠AMD,∠DCN=∠BNC,
∵∠BCD和∠ADC的平分线分别交AB于M,N两点,
∴∠ADM=∠CDM,∠BCN=∠DCN,
∴∠ADM=∠AMD,∠BCN=∠BNC,
∴AD=AM,BC=BN,
∴AM=BN;
(2)解:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,
∴∠CDM=
∠ADC,∠DCN=
∠BCD,
∴∠CDM+∠DCN=
(∠ADC+∠BCD)=90°,
∴∠MON=∠COD=90°,
∵AB=8,BC=6,
∴AM=BN=BC=6,
∴MN=AM+BN-AB=6+6-8=4,
∴OM2+ON2=MN2=16.
∴AB∥CD,AD=BC,
∴∠CDM=∠AMD,∠DCN=∠BNC,
∵∠BCD和∠ADC的平分线分别交AB于M,N两点,
∴∠ADM=∠CDM,∠BCN=∠DCN,
∴∠ADM=∠AMD,∠BCN=∠BNC,
∴AD=AM,BC=BN,
∴AM=BN;
(2)解:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,
∴∠CDM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CDM+∠DCN=
| 1 |
| 2 |
∴∠MON=∠COD=90°,
∵AB=8,BC=6,
∴AM=BN=BC=6,
∴MN=AM+BN-AB=6+6-8=4,
∴OM2+ON2=MN2=16.
点评:此题考查了平行四边形的性质、等腰三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
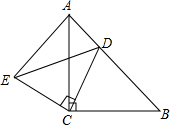 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上. 如图,
如图, 如图,点A表示一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=30°,如果在B、C两村庄之间修一条长500m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?
如图,点A表示一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=30°,如果在B、C两村庄之间修一条长500m的笔直公路将两村连通,那么该公路是否会穿过该森林公园? 如图,∠1=48°,∠3=116°,∠4=64°,求∠2的度数.
如图,∠1=48°,∠3=116°,∠4=64°,求∠2的度数.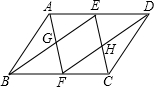 如图,已知?ABCD中,E、F分别为AD、BC的中点,AF与BE交于点G,CE和DF交于点H.说明:EG=HF.
如图,已知?ABCD中,E、F分别为AD、BC的中点,AF与BE交于点G,CE和DF交于点H.说明:EG=HF. 如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出
如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出