题目内容
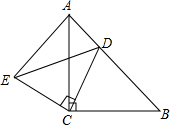 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.(1)求证:△ACE≌△BCD;
(2)若AD=6,BA=14,求ED的长.
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:(1)如图,证明∠ACE=∠BCD,CE=CD,CA=CB,运用SAS公理即可解决问题.
(2)求出AD的长度;证明∠DAE=90°,AE=BD=8,借助勾股定理即可解决问题.
(2)求出AD的长度;证明∠DAE=90°,AE=BD=8,借助勾股定理即可解决问题.
解答: 解:(1)证明:如图,∵△ACB和△ECD均为等腰直角三角形,
解:(1)证明:如图,∵△ACB和△ECD均为等腰直角三角形,
且∠ACB=∠ECD=90°,
∴∠ACE=∠BCD,CE=CD,CA=CB;
在△ACE与△BCD中,
,
∴△ACE≌△BCD(SAS).
(2)∵AD=6,BA=14,
∴BD=14-6=8;
∵△ACE≌△BCD,
∴AE=BD=8;由题意得:∠DAE=45°+45°=90°,
由勾股定理得:DE2=62+82,
∴ED=10.
 解:(1)证明:如图,∵△ACB和△ECD均为等腰直角三角形,
解:(1)证明:如图,∵△ACB和△ECD均为等腰直角三角形,且∠ACB=∠ECD=90°,
∴∠ACE=∠BCD,CE=CD,CA=CB;
在△ACE与△BCD中,
|
∴△ACE≌△BCD(SAS).
(2)∵AD=6,BA=14,
∴BD=14-6=8;
∵△ACE≌△BCD,
∴AE=BD=8;由题意得:∠DAE=45°+45°=90°,
由勾股定理得:DE2=62+82,
∴ED=10.
点评:该题主要考查了等腰直角三角形的性质、勾股定理、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是牢固掌握等腰直角三角形的性质、勾股定理、全等三角形的判定及其性质等几何知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )| A、2 | B、3 | C、4 | D、5 |
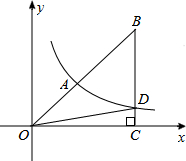 如图,双曲线y=
如图,双曲线y= 如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?
如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?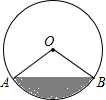 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?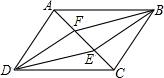 已知E,F是平行四边形ABCD对角线AC上的两个点,BF∥DE,连接DF,BE,则四边形BFDE是平行四边形吗?说明理由.
已知E,F是平行四边形ABCD对角线AC上的两个点,BF∥DE,连接DF,BE,则四边形BFDE是平行四边形吗?说明理由. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?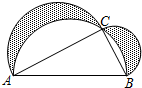 如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.
如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积. 在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.
在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.