题目内容
 如图,点A表示一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=30°,如果在B、C两村庄之间修一条长500m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?
如图,点A表示一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=30°,如果在B、C两村庄之间修一条长500m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?考点:勾股定理的应用
专题:
分析:根据特殊角的三角函数值求出BH=AH和HC=
AH,再根据BC=BH+HC,求出AH的值,再与300进行比较即可得出答案.
| 3 |
解答:解:∵∠B=45°,
∴tan45°=
=1,
∴BH=AH,
∵∠C=30°,
∴tan30°=
=
,
∴HC=
AH,
∴BC=BH+HC=AH+
AH,
∵BC=500,
∴(
+1)AH=500,
∴AH=250(
-1),
∵250(
-1)<300,
∴该公路会穿过该森林公园.
∴tan45°=
| AH |
| BH |
∴BH=AH,
∵∠C=30°,
∴tan30°=
| AH |
| HC |
| ||
| 3 |
∴HC=
| 3 |
∴BC=BH+HC=AH+
| 3 |
∵BC=500,
∴(
| 3 |
∴AH=250(
| 3 |
∵250(
| 3 |
∴该公路会穿过该森林公园.
点评:本题考查了锐角三角函数的定义,利用锐角三角函数的定义求出BH=AH是解答此题的关键.

练习册系列答案
相关题目
 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )| A、2 | B、3 | C、4 | D、5 |
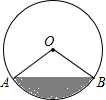 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏? 如图,平行四边形ABCD中,点E、F分别是AD、DC边的中点,BE、BF分别与AC交于R、T.你能发现AR、RT、TC之间的关系吗?
如图,平行四边形ABCD中,点E、F分别是AD、DC边的中点,BE、BF分别与AC交于R、T.你能发现AR、RT、TC之间的关系吗? 如图,
如图, 在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.
在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O. 如图,已知DE是AC的垂直平分线,AB=10cm,BC=14cm,则△ABD的周长为
如图,已知DE是AC的垂直平分线,AB=10cm,BC=14cm,则△ABD的周长为