题目内容
14．求下列各式中的x的值．（x-1）2=$2\frac{1}{4}$．
分析 把（x-1）看作一个整体，然后根据平方根的定义解答即可．
解答 解：∵（x-1）2=$2\frac{1}{4}$=$\frac{9}{4}$，
∴x-1=$\frac{3}{2}$或x-1=-$\frac{3}{2}$，
解得x=$\frac{5}{2}$或x=-$\frac{1}{2}$．
点评 本题考查了利用平方根的定义求未知数的值，难点在于要把（x-1）看作一个整体．
练习册系列答案
相关题目
4．
如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则y的最大值是（ ）
如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则y的最大值是（ ）| A． | 36 | B． | 18 | C． | 20 | D． | 10 |
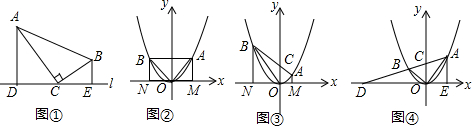
19．原型：如图①，在Rt△ABC中，∠ACB=90°，C是在直线l上的一点，AD⊥l，BE⊥l，垂足分别为D、E．易证△ACD∽△CBE．（不需证明）
应用：点A、B在抛物线y=x2上，且OA⊥OB，连结AB与y轴交于点C，点C的坐标为（0，d）．过点A、B分别作x轴的垂线，垂足为M、N，点M、N的坐标分别为（m，0）、（n，0）．
（1）当OA=OB时，如图②，m=1，d=1；
当OA≠OB，如图③，m=$\frac{2}{3}$时，d=1．
（2）若将抛物线“y=x2”换成“y=2x2”，其他条件不变，当OA=OB时，d=$\frac{1}{2}$；当OA≠OB，m=1时，d=$\frac{1}{2}$．
探究：若将抛物线“y=x2”换成“y=ax2（a＞0）”，其他条件不变，解答下列问题：
（1）完成下列表格．
（2）猜测d与a的关系，并证明其结论．
拓展：如图④，点A、B在抛物线y=ax2（a＞0）上，且OA⊥OB，连结AB与y轴关于点C，AB的延长线与x轴交于点D．AE⊥x轴，垂足为E，当AE=$\frac{4}{3a}$时，△AOE与△CDO的面积之比为4：9．
应用：点A、B在抛物线y=x2上，且OA⊥OB，连结AB与y轴交于点C，点C的坐标为（0，d）．过点A、B分别作x轴的垂线，垂足为M、N，点M、N的坐标分别为（m，0）、（n，0）．
（1）当OA=OB时，如图②，m=1，d=1；
当OA≠OB，如图③，m=$\frac{2}{3}$时，d=1．
（2）若将抛物线“y=x2”换成“y=2x2”，其他条件不变，当OA=OB时，d=$\frac{1}{2}$；当OA≠OB，m=1时，d=$\frac{1}{2}$．
探究：若将抛物线“y=x2”换成“y=ax2（a＞0）”，其他条件不变，解答下列问题：
（1）完成下列表格．
| a | 1 | 2 | 3 | $\frac{1}{2}$ |
| d | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ | 2 |
拓展：如图④，点A、B在抛物线y=ax2（a＞0）上，且OA⊥OB，连结AB与y轴关于点C，AB的延长线与x轴交于点D．AE⊥x轴，垂足为E，当AE=$\frac{4}{3a}$时，△AOE与△CDO的面积之比为4：9．
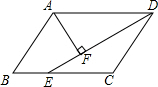如图，?ABCD中，DE平分∠ADC交BC于E，AF⊥DE于F，已知∠DAF=58°，则∠B=64°．