题目内容
已知不等式|x2-5x+6|≤x+a,其中a是实数,若不等式恰有3个整数解,求满足条件的所有的a的值.
考点:一元二次不等式
专题:
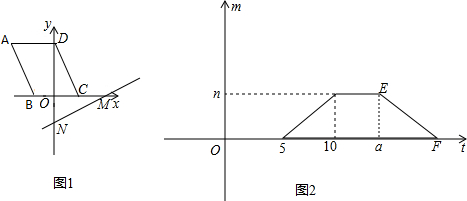
分析:作出二次函数y=|x2-5x+6|的图象,分别求出经过二次函数与x轴的交点,与y轴的交点、过原点的与第一三象限角平分线平行的直线的直线,求得函数的解析式,一次函数与y轴的交点的纵坐标就是a的值,根据函数图象即可判断.
解答: 解:设二次函数y=|x2-5x+6|,令y=0,解得:x=2或3,则函数与x轴的交点是A(2,0)或B(3,0),
解:设二次函数y=|x2-5x+6|,令y=0,解得:x=2或3,则函数与x轴的交点是A(2,0)或B(3,0),
当x=4时,y=2,当x=0时,y=6,则函数一定经过点C(4,2)和点D(0,6).
设一次函数y=x+a,是与第一三象限角平分线平行的直线,
则过A的直线是y=x-2,
过B的直线是y=x-3,
过C的直线是y=x-4,
过D的直线是y=x+6.
则函数的图象如图得:当-2<a≤0时,有三个整数解0,1,2;
当-3≤a≤-2时,有三个整数解是:2,3,4.
总之,a的范围是:-3≤a≤0.
 解:设二次函数y=|x2-5x+6|,令y=0,解得:x=2或3,则函数与x轴的交点是A(2,0)或B(3,0),
解:设二次函数y=|x2-5x+6|,令y=0,解得:x=2或3,则函数与x轴的交点是A(2,0)或B(3,0),当x=4时,y=2,当x=0时,y=6,则函数一定经过点C(4,2)和点D(0,6).
设一次函数y=x+a,是与第一三象限角平分线平行的直线,
则过A的直线是y=x-2,
过B的直线是y=x-3,
过C的直线是y=x-4,
过D的直线是y=x+6.
则函数的图象如图得:当-2<a≤0时,有三个整数解0,1,2;
当-3≤a≤-2时,有三个整数解是:2,3,4.
总之,a的范围是:-3≤a≤0.
点评:本题考查了含有绝对值的二元二次不等式的解法,解题的过程中利用的二次函数的图象,利用了数形结合的思想.

练习册系列答案
相关题目
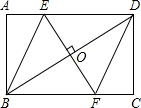 如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF.
如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF. 如图,四边形ABCD是菱形,对角线AC=24,BD=10,过O作OH⊥AB,垂足为H.
如图,四边形ABCD是菱形,对角线AC=24,BD=10,过O作OH⊥AB,垂足为H. 如图,方格纸中每个小正方形的边长为1,△ABC的顶点均在格点上.根据下列要求,利用直尺画图(不写作法):
如图,方格纸中每个小正方形的边长为1,△ABC的顶点均在格点上.根据下列要求,利用直尺画图(不写作法):