题目内容
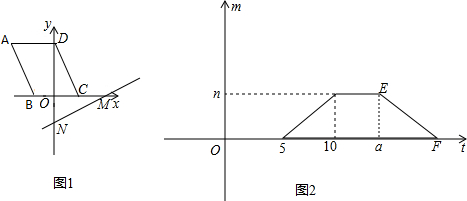
如图①,将?ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左边),点D坐标为(0,4),直线MN:y=
x-6沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图象如图②.
(1)填空:点C的坐标为 ;在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)
(2)点B的坐标为 ,m= ,a= ;
(3)求图②中线段EF的解析式;
(4)t为何值时,该直线平分?ABCD的面积?
| 3 |
| 4 |
(1)填空:点C的坐标为
(2)点B的坐标为
(3)求图②中线段EF的解析式;
(4)t为何值时,该直线平分?ABCD的面积?

考点:一次函数综合题
专题:压轴题
分析:(1)根据直线解析式求出点M、N的坐标,再根据图2判断出CM的长,然后求出OC,从而得到点C的坐标,根据被截线段在一段时间内长度不变可以判断出先经过点B后经过点D;
(2)根据图2求出BM=10,再求出OB,然后写出点B的坐标,利用勾股定理列式求出CD,再求出BC的长度,从而得到BC=CD,判断出?ABCD是菱形,再求出MN⊥CD,根据菱形的性质可知n=DO,根据向左平移横坐标减表示出平移后的直线解析式,把点D的坐标代入函数解析式求出t的值即为a;
(3)根据菱形的性质写出点A的坐标,再求出F的坐标,然后设直线EF的解析式为y=kx+b,再利用待定系数法求一次函数解析式解答;
(4)根据过平行四边形中心的直线平分平行四边形的面积,求出菱形的中心坐标,然后代入直线MN的解析式计算即可得解.
(2)根据图2求出BM=10,再求出OB,然后写出点B的坐标,利用勾股定理列式求出CD,再求出BC的长度,从而得到BC=CD,判断出?ABCD是菱形,再求出MN⊥CD,根据菱形的性质可知n=DO,根据向左平移横坐标减表示出平移后的直线解析式,把点D的坐标代入函数解析式求出t的值即为a;
(3)根据菱形的性质写出点A的坐标,再求出F的坐标,然后设直线EF的解析式为y=kx+b,再利用待定系数法求一次函数解析式解答;
(4)根据过平行四边形中心的直线平分平行四边形的面积,求出菱形的中心坐标,然后代入直线MN的解析式计算即可得解.
解答:解:(1)令y=0,则
x-6=0,解得x=8,
令x=0,则y=-6,
∴点M(8,0),N(0,-6),
∴OM=8,ON=6,
由图2可知5秒后直线经过点C,
∴CM=5,OC=OM-CM=8-5=3,
∴C(3,0),
∵10秒~a秒被截线段长度不变,
∴先经过点B;
(2)由图2可知BM=10,
∴OB=BM-OM=10-8=2,
∴B(-2,0),
在Rt△OCD中,由勾股定理得,CD=
=
=5,
∴BC=CD=5,
∴?ABCD是菱形,
∵
=
=
,
∴MN⊥CD,
∴m=DO=4,
∵设直线MN向x轴负方向平移的速度为每秒1个单位的长度,
平移后的直线解析式为y=
(x+t)-6,
把点D(0,4)代入得,
(0+t)-6=4,
解得t=
,
∴a=
;
故答案为:(1)(3,0),B;(2)(-2,0),4,
;
(3)由(2)可得点E的坐标为(
,4),
由菱形的性质,点A(-5,4),
代入直线平移后的解析式得,
(-5+t)-6=4,
解得t=
,
∴点F(
,0)
设直线EF的解析式为y=kx+b,
则
,
解得
,
所以线段EF的解析式为:y=-
x+
;
(4)∵B(-2,0),D(0,4),
∴?ABCD的中心坐标为(-1,2),
∵直线M平分?ABCD的面积,
∴直线MN经过中心坐标,
∴
(-1+t)-6=2,
解得t=
,
即t=
时,该直线平分?ABCD的面积.
| 3 |
| 4 |
令x=0,则y=-6,
∴点M(8,0),N(0,-6),
∴OM=8,ON=6,
由图2可知5秒后直线经过点C,
∴CM=5,OC=OM-CM=8-5=3,
∴C(3,0),
∵10秒~a秒被截线段长度不变,
∴先经过点B;
(2)由图2可知BM=10,
∴OB=BM-OM=10-8=2,
∴B(-2,0),
在Rt△OCD中,由勾股定理得,CD=
| OD2+OC2 |
| 42+32 |
∴BC=CD=5,
∴?ABCD是菱形,
∵
| OC |
| OD |
| ON |
| OM |
| 3 |
| 4 |
∴MN⊥CD,
∴m=DO=4,
∵设直线MN向x轴负方向平移的速度为每秒1个单位的长度,
平移后的直线解析式为y=
| 3 |
| 4 |
把点D(0,4)代入得,
| 3 |
| 4 |
解得t=
| 40 |
| 3 |
∴a=
| 40 |
| 3 |
故答案为:(1)(3,0),B;(2)(-2,0),4,
| 40 |
| 3 |
(3)由(2)可得点E的坐标为(
| 40 |
| 3 |
由菱形的性质,点A(-5,4),
代入直线平移后的解析式得,
| 3 |
| 4 |
解得t=
| 55 |
| 3 |
∴点F(
| 55 |
| 3 |
设直线EF的解析式为y=kx+b,
则
|
解得
|
所以线段EF的解析式为:y=-
| 4 |
| 5 |
| 44 |
| 3 |
(4)∵B(-2,0),D(0,4),
∴?ABCD的中心坐标为(-1,2),
∵直线M平分?ABCD的面积,
∴直线MN经过中心坐标,
∴
| 3 |
| 4 |
解得t=
| 35 |
| 3 |
即t=
| 35 |
| 3 |
点评:本题是一次函数综合题型,主要利用了平行四边形的性质,菱形的判定与性质,一次函数图象的平移待定系数法求一次函数解析式,表示出平移后的直线MN的解析式是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用配方法解方程-x2+6x+7=0,可变形为( )
| A、(x+3)2=16 |
| B、(x-3)2=16 |
| C、(x+3)2=2 |
| D、(x-3)2=2 |
 已知∠ABC,点P在射线BA上,请根据“同位角相等,两直线平行”,利用直尺和圆规,过点P作直线PD平行于BC.(保留作图痕迹,不写作法)
已知∠ABC,点P在射线BA上,请根据“同位角相等,两直线平行”,利用直尺和圆规,过点P作直线PD平行于BC.(保留作图痕迹,不写作法) 如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从A出发沿射线AB以1cm/s的速度作直线运动,点Q从C出发沿边BC的延长线以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,△PCQ的面积为24cm2?
如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从A出发沿射线AB以1cm/s的速度作直线运动,点Q从C出发沿边BC的延长线以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,△PCQ的面积为24cm2? 请将图中数轴上标有字母的各点与下列实数对应起来,再把下列各数用“>”连接起来.
请将图中数轴上标有字母的各点与下列实数对应起来,再把下列各数用“>”连接起来.