Question

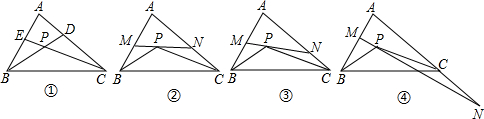
如图①，△ABC的角平分线BD、CE相交于点P．
（1）如果∠A=70°，求∠BPC的度数；
（2）如图②，过P点作直线MN∥BC，分别交AB和AC于点M和N，试求∠MPB+∠NPC的度数（用含∠A的代数式表示）；
（3）在（2）的条件下，将直线MN绕点P旋转．
（i）当直线MN与AB、AC的交点仍分别在线段AB和AC上时，如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由；
（ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（i）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若成立，请说明你的理由；若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由．

Answer 1

考点：三角形内角和定理,平行线的性质,三角形的外角性质

专题：计算题

分析：（1）根据三角形内角和定理得到∠BPC=180°-∠PBC-∠PCB，再根据角平分线定义得到∠BPC=180°-（

1

2

∠ABC+

1

2

∠ACB），再利用三角形内角和定理得∠BPC=180°-

1

2

（180°-∠A）=90°+

1

2

∠A，然后把∠A的度数代入计算；
（2）根据平角定义得∠MPB+∠NPC=180°-∠BPC，然后根据（1）的求解；
（3）（ i）∠与（2）的说理一样；
（ⅱ）有结论∠MPB-∠NPC=90°-

1

2

∠A．

解答：解：（1）∠BPC=180°-∠PBC-∠PCB
=180°-（

1

2

∠ABC+

1

2

∠ACB）
=180°-

1

2

（180°-∠A）
=90°+

1

2

∠A
=90°+

1

2

×70°
=125°；
（2）∵∠BPC=90°+

1

2

∠A，
∴∠MPB+∠NPC=180°-∠BPC=180°-（90°+

1

2

∠A）=90°-

1

2

∠A；
（3）（ i）∠MPB+∠NPC=90°-

1

2

∠A．理由如下：
∵∠BPC=90°+

1

2

∠A，
∴∠MPB+∠NPC=180°-∠BPC=180°-（90°+

1

2

∠A）
=90°-

1

2

∠A；
（ⅱ）不成立，有∠MPB-∠NPC=90°-

1

2

∠A．
理由如下：由图可知∠MPB+∠BPC-∠NPC=180°，
由（i）知：∠BPC=90°+

1

2

∠A，
∴∠MPB-∠NPC=180°-∠BPC
=180°-（90°+

1

2

∠A）
=90°-

1

2

∠A．

点评：本题考查了三角形内角和定理：三角形内角和是180°．也考查了平角的定义．