题目内容
10.已知实数x,y满足:x4+x2=3,$\frac{4}{{y}^{4}}$+$\frac{2}{{y}^{2}}$=3,则x4+$\frac{4}{{y}^{4}}$=7.分析 把已知条件变形得到4($\frac{1}{{y}^{2}}$)2+2•$\frac{1}{{y}^{2}}$-3=0,x4+x2-3=0,则x2和$\frac{1}{{y}^{2}}$可看作方程t2+t-3=0的两根,根据根与系数的关系得到x2+$\frac{1}{{y}^{2}}$=-1,x2•$\frac{1}{{y}^{2}}$=-3,再利用完全批发公司变形得到x4+$\frac{4}{{y}^{4}}$=(x2+$\frac{1}{{y}^{2}}$)2-2x2•$\frac{1}{{y}^{2}}$,然后利用整体代入的方法计算.
解答 解:∵$\frac{4}{{y}^{4}}$+$\frac{2}{{y}^{2}}$=3,
∴4($\frac{1}{{y}^{2}}$)2+2•$\frac{1}{{y}^{2}}$-3=0,
而x4+x2-3=0,
∴x2和$\frac{1}{{y}^{2}}$可看作方程t2+t-3=0的两根,
∴x2+$\frac{1}{{y}^{2}}$=-1,x2•$\frac{1}{{y}^{2}}$=-3,
∴x4+$\frac{4}{{y}^{4}}$=(x2+$\frac{1}{{y}^{2}}$)2-2x2•$\frac{1}{{y}^{2}}$=1-2×(-3)=7.
故答案为7.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.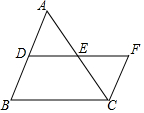 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )| A. | 1:3 | B. | 2:3 | C. | 2:5 | D. | 1:4 |
2.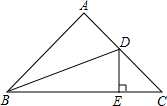 在45°的Rt△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且BD=13,AB=12,则△DEC的周长为( )
在45°的Rt△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且BD=13,AB=12,则△DEC的周长为( )
 在45°的Rt△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且BD=13,AB=12,则△DEC的周长为( )
在45°的Rt△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且BD=13,AB=12,则△DEC的周长为( )| A. | 10$\sqrt{2}$ | B. | 5+$\sqrt{2}$ | C. | 10+$\sqrt{2}$ | D. | 17 |
 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.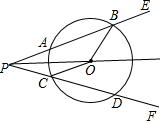 如图,已知点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证:
如图,已知点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证: 如图∠AED=∠C,∠DEF=∠B,试说明∠1+∠2=180°.
如图∠AED=∠C,∠DEF=∠B,试说明∠1+∠2=180°. 如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AC}$=$\frac{AE}{AB}$,∠BAC的平分线AG分别交线段DE、BC于点F、G.
如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AC}$=$\frac{AE}{AB}$,∠BAC的平分线AG分别交线段DE、BC于点F、G.