题目内容
5.把一根绳子对折后,从它对折后的中间剪断,就成了3段,把一根绳子对折后再对折,从第二次对折后的中间剪断,就成了5段,把一条绳子对折3次后,从它第3次对折后的中间剪断,就成了9段,从它第4次对折后的中间剪断,就成了33段;如果从它第n次对折后的中间剪断,那么这条绳子会被剪成2n+1段.分析 根据有理数的乘方,写成2的指数幂的形式,然后得到规律即可得解.
解答 解:对折后的中间剪断,就成了3段,3=21+1,
从第二次对折后的中间剪断,就成了5段,5=22+1,
从它第3次对折后的中间剪断,就成了9段,9=23+1,
…,
依此类推,从它第n次对折后的中间剪断,那么这条绳子会被剪成2n+1段.
当n=4时,24+1=33,
故答案为:33,2n+1.
点评 本题考查了有理数的乘方及图形的变化类问题,读懂题目信息,并理解有理数的乘方的意义是解题的关键,解决本题的难点是正确的找到题目中的规律.

练习册系列答案
相关题目
20.正方形ABCD中,E,F分别为AB,BC的中点,AF与DE相交于点O,则$\frac{DO}{AD}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$$\sqrt{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
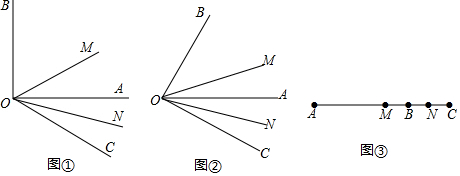
 如图,已知OC平分∠AOB,CD∥OB,若OD=6cm,则CD的长等于6cm.
如图,已知OC平分∠AOB,CD∥OB,若OD=6cm,则CD的长等于6cm.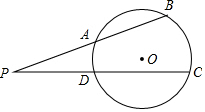 如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.