题目内容
2.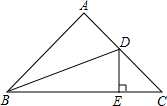 在45°的Rt△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且BD=13,AB=12,则△DEC的周长为( )
在45°的Rt△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且BD=13,AB=12,则△DEC的周长为( )| A. | 10$\sqrt{2}$ | B. | 5+$\sqrt{2}$ | C. | 10+$\sqrt{2}$ | D. | 17 |
分析 根据已知求出AC、EC,DE=AD,求出△ADE的周长=AC+CE,代入求出即可.
解答 解:∵AB=AC,∠A=90°,DE⊥BC,BD是∠ABC的平分线,
∴BE=AB=AC=12,
∵BD=13,
∴DE=AD=5,
∵∠C=45°,
∴CE=5,
BC=12$\sqrt{2}$
∴△DEC的周长是DE+CE+DC=AD+CE+CD=AC+CE=12+5=17.
故选D.
点评 本题考查了等腰直角三角形,角平分线性质,勾股定理的应用,关键是求出△DEC的周长=AC+CE.

练习册系列答案
相关题目
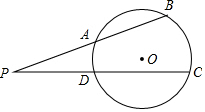 如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )