题目内容
1.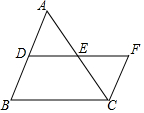 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )| A. | 1:3 | B. | 2:3 | C. | 2:5 | D. | 1:4 |
分析 先利用SAS证明△ADE≌△CFE得出S△ADE=S△CFE,再由DE为中位线,判断△ADE∽△ABC,且相似比为1:2,利用相似三角形的面积比等于相似比,得到S△ADE:S△ABC=1:4,则即$\frac{{S}_{△ADE}}{{S}_{△ADE}+{S}_{四边形BCED}}$=$\frac{{S}_{△ADE}}{{S}_{△CFE}+{S}_{四边形BCED}}$=$\frac{{S}_{△ADE}}{{S}_{四边形BCFD}}$=$\frac{1}{4}$.
解答 解:∵DE为△ABC的中位线,
∴AE=CE.
在△ADE与△CFE中,
∵$\left\{\begin{array}{l}{AE=CE}\\{∠AED=∠CEF}\\{DE=FE}\end{array}\right.$,
∴△ADE≌△CFE(SAS),
∴S△ADE=S△CFE.
∵DE为△ABC的中位线,
∴△ADE∽△ABC,且相似比为1:2,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{4}$,即$\frac{{S}_{△ADE}}{{S}_{△ADE}+{S}_{四边形BCED}}$=$\frac{{S}_{△ADE}}{{S}_{△CFE}+{S}_{四边形BCED}}$=$\frac{{S}_{△ADE}}{{S}_{四边形BCFD}}$=$\frac{1}{4}$,
故选:D.
点评 本题考查了全等三角形、相似三角形的判定与性质,三角形中位线定理.关键是利用中位线定理判断相似三角形及相似比.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
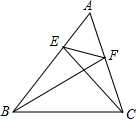 如图,△ABC中,CE⊥AB,BF⊥AC,若∠A=60°,BC=4,则EF的长为2.
如图,△ABC中,CE⊥AB,BF⊥AC,若∠A=60°,BC=4,则EF的长为2.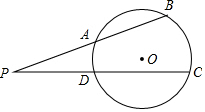 如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.