题目内容
8.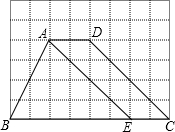 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(2)请直接写出△AEF与四边形ABCD重叠部分的面积.
答:△AEF与四边形ABCD重叠部分的面积是6.
分析 (1)根据AE为网格正方形的对角线,作出点B关于AE的对称点F,然后连接AF、EF即可;
(2)根据图形,重叠部分为两个直角三角形的面积的差,列式计算即可得解.
解答 解:(1)△AEF如图所示;
(2)重叠部分的面积=$\frac{1}{2}$×4×4-$\frac{1}{2}$×2×2
=8-2
=6.
故答案为:6.
点评 本题考查了利用轴对称变换作图,熟练掌握网格结构并观察出AE为网格正方形的对角线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.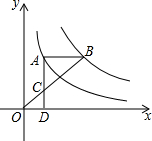 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
19.以下列长度的线段为边能构成直角三角形的是( )
| A. | 1,2,3 | B. | 6,8,12 | C. | 5,12,5 | D. | 7,24,25 |
16.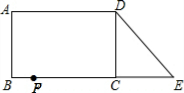 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.| A. | 1 | B. | 1或3 | C. | 1或7 | D. | 3或7 |
13.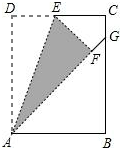 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{3}$ |
20.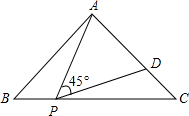 如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
 如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )| A. | 10-3$\sqrt{2}$ | B. | 10-2$\sqrt{3}$ | C. | 4 | D. | 6 |