题目内容
3.高盛超市准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.(1)超市若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(2)超市若要获得最大利润,则每个定价多少元?获得的最大利润是多少?
分析 (1)设每个定价增加x元,根据总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍,即可得出答案;
(2)利用函数的性质求最值,即可得出答案.
解答 解:(1)设每个定价增加x元,根据题意得:
(x+10)(400-10x)=6000,
整理得:x2-30x+200=0
解得x1=10,x2=20,
∵进货量较少,
∴x=20,
∴每个定价为50+20=70(元),
进货量为:400-10x=400-200=200(个).
答:当定价为70元时利润达到6000元,此时的进货量为200个;
(2)设最大利润为y元,则y=-10x2+300x+4000,
当x=-$\frac{300}{-20}$=15时,y最大=4000-$\frac{90000}{-40}$=6250.
所以每个定价为65元时,获得的最大利润为6250元.
点评 此题主要考查了二次函数的应用,注意应用题中求最值需先求函数表达式,再运用函数性质求解.此题的关键在列式表示销售价格和销售量.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
13.如果$\sqrt{\frac{x-1}{y}}$是二次根式,那么x,y应满足的条件是( )
| A. | x≥1,y≥0 | B. | (x-1)•y≥0 | C. | $\frac{x-1}{y}$≥0 | D. | x≥1,y>0 |
14.下列方程组中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{xy=2}\\{x+y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+y=1}\\{\frac{{x}^{2}}{x}+y=-2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{\frac{x}{2}-\frac{y}{4}=1}\end{array}\right.$ |
15.用一个平面去截一个几何体,截面的形状是三角形,那么这个几何体不可能是( )
| A. | 圆锥 | B. | 五棱柱 | C. | 正方体 | D. | 圆柱 |
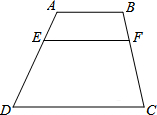 如图,AB∥EF∥CD,AB=3,CD=7,AE:ED=1:3,则EF的长度为4.
如图,AB∥EF∥CD,AB=3,CD=7,AE:ED=1:3,则EF的长度为4.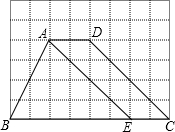 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE. 如图,已知AB为⊙O的直径,CD⊥AB于点D,交⊙O于点F,AC交⊙O于点E,BE交CD于点G.求证:FD2=CD•GD.
如图,已知AB为⊙O的直径,CD⊥AB于点D,交⊙O于点F,AC交⊙O于点E,BE交CD于点G.求证:FD2=CD•GD.