题目内容
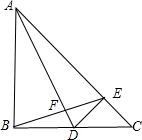已知如图，△ABC中，∠ABC=90°，AB=BC，D是BC边上一点，DE⊥AC于E，连BE交AD与F．（1）如果
| BC |
| BD |
| CE |
| AC |
（2）如果
| BC |
| BD |
| EF |
| BF |
（3）如果
| BC |
| BD |
| EF |
| BF |
考点：相似三角形的判定与性质,勾股定理
专题：计算题
分析：（1）设AB=BC=3a，利用勾股定理求得AC．利用AB=BC，可得∠C=45°，再利用DE⊥AC于E，可得DE=CE=
a，然后根据
=3即可求得
的值；
（2）作EG⊥BC交AD于G，可得
=
=
，再利用
=3，即可求出
的值；
（3）根据
=n，可直接得出
的值．
| 2 |
| BC |
| BD |
| CE |
| AC |
（2）作EG⊥BC交AD于G，可得
| EG |
| CD |
| AE |
| AC |
| 2 |
| 3 |
| BC |
| BD |
| EF |
| BF |
（3）根据
| BC |
| BD |
| EF |
| BF |
解答：解：（1）设AB=BC=3a，
∵∠ABC=90°
∴AC=
=3
a，
又∵AB=BC，DE⊥AC于E
∴∠C=∠BAC=45°，∠EDC=45°，
∴DE=CE
∵
=3，
∴DE=CE=
a，
∴
=
．
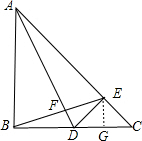
（2）作EG⊥BC交AD于G，
∴
=
=
，
∵
=3，
∴
=
，
∴
=
=
，
（3）∵
=n，
∴
=
．
∵∠ABC=90°
∴AC=
| AB2+BC2 |
| 2 |
又∵AB=BC，DE⊥AC于E
∴∠C=∠BAC=45°，∠EDC=45°，
∴DE=CE
∵
| BC |
| BD |
∴DE=CE=
| 2 |
∴
| CE |
| AC |
| 1 |
| 3 |
（2）作EG⊥BC交AD于G，
∴
| EG |
| CD |
| AE |
| AC |
| 1 |
| 2 |
∵
| BC |
| BD |
∴
| EG |
| BD |
| 4 |
| 3 |
∴
| EF |
| BF |
| EG |
| BD |
| 4 |
| 3 |
（3）∵
| BC |
| BD |
∴
| EF |
| BF |
| n2-1 |
| 2n |
点评：此题主要考查勾股定理和相似三角形的判定与性质等知识点，有一定的拔高难度，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
小马在计算“41+x”时，误将“+”看成“-”，结果得12，则41+x的值应为（ ）
| A、29 | B、53 | C、67 | D、70 |
如图，∠MAB+∠NBA=130°，则∠C+∠D的值是（ ）| A、130° | B、150° |
| C、135° | D、90° |