题目内容
5.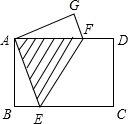 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是$\frac{25}{16}$.
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是$\frac{25}{16}$.
分析 要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求AE.
解答 解:设AE=x,由折叠可知,EC=x,BE=4-x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4-x)2=x2,
解得:x=$\frac{25}{8}$
由折叠可知∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF=$\frac{25}{8}$,
∴S△AEF=$\frac{1}{2}$×AF×AB=$\frac{1}{2}$×$\frac{25}{8}$×3=$\frac{75}{16}$.
故答案为:$\frac{75}{16}$.
点评 本题考查的是图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
8. 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )| A. | x<2 | B. | x>2 | C. | x<-1 | D. | x>-1 |
5.将某班级全体同学按课外阅读的不同兴趣分成三组,情况如表格所示,则表中a的值应该是7.
| 第一组 | 第二组 | 第三组 | |
| 频数 | 12 | 16 | a |
| 频率 | b | c | 20% |
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=4,DB=3,BC=9,则DE的长为$\frac{36}{7}$.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=4,DB=3,BC=9,则DE的长为$\frac{36}{7}$. 如图,A,B两地之间有一座山,汽车原来从A地道B地须经C地沿折线A-C-B行驶,全长68km,现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,A,B两地之间有一座山,汽车原来从A地道B地须经C地沿折线A-C-B行驶,全长68km,现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)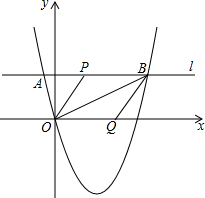 如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.
如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.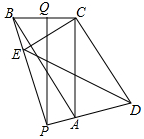 如图,△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于P点,Q是BC的中点,连PQ在旋转过程中,PQ最大值是( )
如图,△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于P点,Q是BC的中点,连PQ在旋转过程中,PQ最大值是( ) 为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成两幅不完整的统计图如图所示,则抽查的学生中户外活动时间为1.5小时的人数12.
为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成两幅不完整的统计图如图所示,则抽查的学生中户外活动时间为1.5小时的人数12. 在某次学校安全知识抢答赛中,九年级参赛的10名学生的成绩统计图如图所示.这10名学生的参赛成绩的中位数是90分.
在某次学校安全知识抢答赛中,九年级参赛的10名学生的成绩统计图如图所示.这10名学生的参赛成绩的中位数是90分.