题目内容
12.在等腰△ABC中,两条边长分别为3和4,则等腰△ABC的周长等于10或11;等腰三角形的一个角为100°,则它的底角为40°,40°.分析 由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析.
根据等腰三角形两底角相等列式计算即可得解.
解答 解:①3是腰长时,三角形的三边分别为3、3、4,
能组成三角形,周长=3+3+4=10,
②3是底边长时,三角形的三边分别为3、4、4,
能组成三角形,周长=3+4+4=11,
综上所述,这个等腰三角形的周长是10或11.
∵等腰三角形的一个角为100°,
∴100°的角是顶角,底角为$\frac{1}{2}$(180°-100°)=40°.
故答案为:10或11;40°,40°.
点评 本题考查了等腰三角形的性质,第二问难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形.

练习册系列答案
相关题目
19.“4的平方根是±2”的翻译成数学表达式是( )
| A. | $\sqrt{4}$=±2 | B. | -$\sqrt{4}$=2 | C. | -$\sqrt{4}$=2 | D. | ±$\sqrt{4}$=±2 |
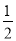 BC,连结DE,CF。
BC,连结DE,CF。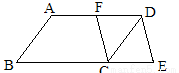
 如图,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE,请你判断AC垂直于CE吗?并说明理由.
如图,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE,请你判断AC垂直于CE吗?并说明理由.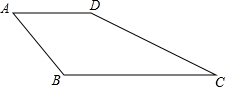 在四边形ABCD中,AB=AD=2,∠A=60°,BC=2$\sqrt{5}$,CD=4.求∠ADC的度数.
在四边形ABCD中,AB=AD=2,∠A=60°,BC=2$\sqrt{5}$,CD=4.求∠ADC的度数. 如图,已知A1(1,0)、A2(1,-1)、A3(-1,-1))、A4(-1,1)、A5(2,1)、…,则点A2015的坐标是(-504,-504).
如图,已知A1(1,0)、A2(1,-1)、A3(-1,-1))、A4(-1,1)、A5(2,1)、…,则点A2015的坐标是(-504,-504).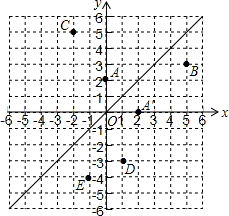 如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.