题目内容
7.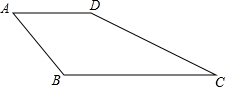 在四边形ABCD中,AB=AD=2,∠A=60°,BC=2$\sqrt{5}$,CD=4.求∠ADC的度数.
在四边形ABCD中,AB=AD=2,∠A=60°,BC=2$\sqrt{5}$,CD=4.求∠ADC的度数.
分析 连接BD,根据AB=AD=2,∠A=60°,得出△ABD是等边三角形,求得BD=2,然后根据勾股定理的逆定理判断三角形BDC是直角三角形,从而求得∠ADC=150°.
解答 解:连接BD,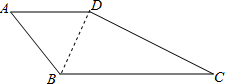
∵AB=AD=2,∠A=60°,
∴△ABD是等边三角形,
∴BD=2,∠ADB=60°,
∵BC=2$\sqrt{5}$,CD=4,
则BD2+CD2=22+42=20,BC2=(2$\sqrt{5}$)2=20,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=150°.
点评 本题考查了等边三角形的判定和性质,直角三角形的判定和性质,关键是根据勾股定理的逆定理判断三角形BDC是直角三角形.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
15.下列分解因式正确的是( )
| A. | x2+y2=(x+y)(x-y) | B. | m2-2m+1=(m+1)2 | C. | (a+4)(a-4)=a2-16 | D. | x3-x=x(x2-1) |
19.为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
| A. | 总体 | B. | 个体 | C. | 总体的一个样本 | D. | 普查方式 |
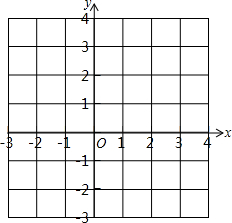 如图,已知O是坐标原点,A、B两点的坐标分别为(3,-1)、(2,1).
如图,已知O是坐标原点,A、B两点的坐标分别为(3,-1)、(2,1).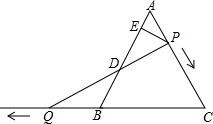 如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.
如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.