题目内容
17．解不等式组：$\left\{\begin{array}{l}{x-3（x-2）≤4}\\{\frac{1+2x}{3}＞x-1}\end{array}\right.$，并指出它的所有整数解．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集，然后确定解集中的整数解即可．
解答 解：$\left\{\begin{array}{l}{x-3（x-2）≤4…①}\\{\frac{1+2x}{3}＞x-1…②}\end{array}\right.$，
解①得：x≥1，
解②得：x＜4．
则不等式组的解集是：1≤x＜4．
则整数解是：1，2，3．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
名校课堂系列答案
相关题目
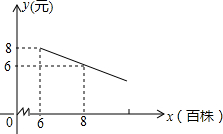某花店计划用100个花盆培育一种花卉，用于国庆销售，已知花店从批发市场购进花苗的单价为y（元）和数量x（百株）之间的关系如图所示（其中x≥6），根据以往经验，每年的花卉供不应求，但若每个花盆培育6株，每株的销售单价为26元，每个花盆每增加1株，每株的销售单价就减少2元．
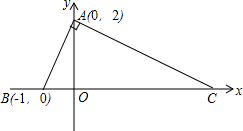如图，平面直角坐标系中，AB⊥AC，
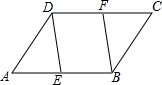在?ABCD中，点E、F分别在AB、CD上，∠DEA=∠BFC，求证：四边形DEBF为平行四边形．
2．解关于x的不等式组$\left\{\begin{array}{l}{x-a＜0}\\{7-2x≤2}\end{array}\right.$的整数解有4个，则a的取值范围是（ ）
| A． | 6＜a＜7 | B． | 6≤a＜7 | C． | 6≤a≤7 | D． | 6＜a≤7 |
9．下列各组数中，不能构成直角三角形的一组是（ ）
| A． | 3，4，5 | B． | 1，2，$\sqrt{3}$ | C． | 5，12，13 | D． | 6，8，12 |
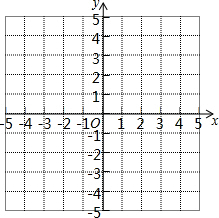如图，在平面直角坐标系中，O为坐标原点，△ABC的三个顶点坐标分别为A（-1，-2），B（1，1），C（-3，1），△A1B1C1是△ABC向下平移2个单位，向右平移3个单位得到的．