题目内容
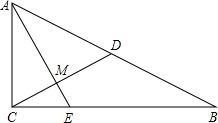 在Rt△ABC中,∠ACB=90°,D在AB中点,AE⊥CD于点M,
在Rt△ABC中,∠ACB=90°,D在AB中点,AE⊥CD于点M,(1)求证:△ACM∽△BAC;
(2)若2CE=BE,CD=2
| 3 |
考点:相似三角形的判定与性质
专题:
分析:(1)利用直角三角形斜边上的中线等于斜边的一半可得到∠DAC=∠DCA,结合垂直可证得△ACM∽△BAC;
(2)由(1)可得到∠CAM=∠B,可证得△ACE∽△BCA,可得到AC和BC之间的关系,再结合条件利用勾股定理得到AC和BC之间的关系,可求得AC.
(2)由(1)可得到∠CAM=∠B,可证得△ACE∽△BCA,可得到AC和BC之间的关系,再结合条件利用勾股定理得到AC和BC之间的关系,可求得AC.
解答:(1)证明:
∵D为AB中点,且∠ACB=90°,
∴DA=DC,
∴∠ACM=∠BAC,
∵AE⊥CD,
∴∠AMC=∠ACB=90°,
∴△ACM∽△BAC;
(2)解:由(1)可知△ACM∽△BAC,
∴∠CAM=∠B,且∠ACE=∠BCA,
∴△ACE∽△BCA,
∴
=
,又BC=2CE,
∴AC2=
BC2,即BC2=2AC2,
∵CD=2
,
∴AB=2CD=4
,
又AC2+BC2=AB2,
∴3AC2=48,
∴AC=4.
∵D为AB中点,且∠ACB=90°,
∴DA=DC,
∴∠ACM=∠BAC,
∵AE⊥CD,
∴∠AMC=∠ACB=90°,
∴△ACM∽△BAC;
(2)解:由(1)可知△ACM∽△BAC,
∴∠CAM=∠B,且∠ACE=∠BCA,
∴△ACE∽△BCA,
∴
| CE |
| AC |
| AC |
| BC |
∴AC2=
| 1 |
| 2 |
∵CD=2
| 3 |
∴AB=2CD=4
| 3 |
又AC2+BC2=AB2,
∴3AC2=48,
∴AC=4.
点评:本题主要考查相似三角形的判定和性质,利用相似三角形可得到角相等,可为证明相似寻找条件,这也是解题过程中的常用思路,注意勾股定理的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
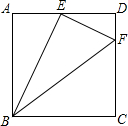 如图,在□ABCD中,E是AD的中点,F是CD上一点,且CF=3FD.图中有几对相似三角形?把它们表示出来,并说明理由.
如图,在□ABCD中,E是AD的中点,F是CD上一点,且CF=3FD.图中有几对相似三角形?把它们表示出来,并说明理由. 如图,在⊙O中,弦AB,CD相交于点P,且AB=CD,求证:AC=BD.
如图,在⊙O中,弦AB,CD相交于点P,且AB=CD,求证:AC=BD.