题目内容
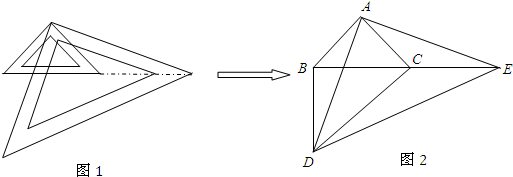
18．
如图所示，在一条河的同岸有两个村庄A和B，两村要在河上合修一座桥，桥修在什么地方，可以使两个村庄到桥的距离之和最短？
分析 画出点A关于直线m的对称点A′，连接A′B交m于点C，连接AC，由对称的性质可知AC=A′C，由两点之间线段最短可知点C即为所求点．
解答 解：画出点A关于直线m的对称点A′，连接A′B交m于点C，连接AC，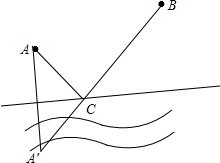
∵A、A′关于直线m对称，
∴AC=A′C，
∴AC+BC=A′B，
由两点之间线段最短可知，线段A′B的长即为AC+BC的最小值，故C点即为所求点．
点评 本题考查的是最短线路问题，熟知对称的性质及两点之间线段最短的知识是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．
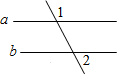如图，已知∠1=100°，若要使a∥b，则∠2=（ ）
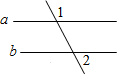如图，已知∠1=100°，若要使a∥b，则∠2=（ ）| A． | 100° | B． | 60° | C． | 40° | D． | 80° |
6．
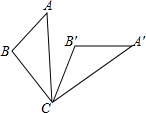如图，将△ABC绕着点C顺时针旋转60°后得到△A′B′C，若∠A=40°，∠B=110°，则∠BCA′的度数是（ ）
如图，将△ABC绕着点C顺时针旋转60°后得到△A′B′C，若∠A=40°，∠B=110°，则∠BCA′的度数是（ ）| A． | 100° | B． | 90° | C． | 70° | D． | 110° |
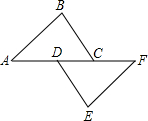如图，在△ABC和△FED中，AD=FC，AB=FE，BC=ED，求证：
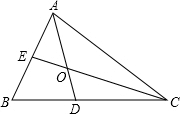如图，在△ABC中，∠B=60°，∠BAC、∠BCA的平分线AD，CE交于点O，猜想OE与OD的大小关系和AC与AE、CD的大小关系，并说出你的理由．