题目内容
10.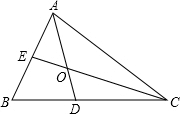 如图,在△ABC中,∠B=60°,∠BAC、∠BCA的平分线AD,CE交于点O,猜想OE与OD的大小关系和AC与AE、CD的大小关系,并说出你的理由.
如图,在△ABC中,∠B=60°,∠BAC、∠BCA的平分线AD,CE交于点O,猜想OE与OD的大小关系和AC与AE、CD的大小关系,并说出你的理由.
分析 连接OB,先求出∠ABC+∠DOE=180°,证出B、D、O、E四点共圆,得出$\widehat{OE}=\widehat{OD}$,即可得出OE=OD;
在CA上取点G,使得CG=CD,连接OG,先证明△GCO≌△DCO,得出∠GOC=∠COD=60°,CD=CG求出∠AOG=∠AOE,再证明△AEO≌△AGO,得出AE=AG,即可得出结论.
解答 解:OE=OD;理由:连接OB,如图所示:
∵∠ABC=60°,
∴∠BAC+∠ACB=120°,
∵∠BAC、∠BCA的平分线AD,CE交于点O,
∴∠OAC+∠OCA=$\frac{1}{2}$(∠BAC+∠ACB)=60°,OB平分∠ABC,
∴∠DOE=∠AOC=180°-(∠OAC+∠OCA)=120°,∠ABO=∠DBO=30°,
∴∠ABC+∠DOE=180°,
∴B、D、O、E四点共圆,
∴$\widehat{OE}=\widehat{OD}$,
∴OE=OD;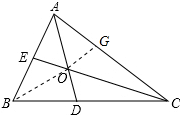
AC=AE+CD;理由:
在CA上取点G,使得CG=CD,连接OG,如图所示:
∵∠AOC=180°-$\frac{1}{2}$(∠BAC+∠ACB)=180°-$\frac{1}{2}$(180°-60°)=120°,
∴∠AOE=∠COD=60°,
∵在△GCO和△DCO中,$\left\{\begin{array}{l}{OC=OC}&{\;}\\{∠GCO=∠OCD}&{\;}\\{CG=CD}&{\;}\end{array}\right.$,
∴△GCO≌△DCO(SAS),
∴∠GOC=∠COD=60°,
∴∠AOG=120°-60°=60°=∠AOE,
∵在△AEO和△AGO中,$\left\{\begin{array}{l}{∠AOE=∠AOG}&{\;}\\{∠EAO=∠GAO}&{\;}\\{AO=AO}&{\;}\end{array}\right.$,
∴△AEO≌△AGO(AAS),
∴AE=AG,
∴AE+CD=AG+CG=AC.
点评 本题考查四点共圆、全等三角形的判定与性质、圆周角定理的推论、角平分线的运用以及三角形内角和定理;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
| A. | sin45° | B. | $\frac{1}{3}$ | C. | 0.3 | D. | 3.14 |
 实数a,b在数轴上对应点的位置如图所示,下列各式中正确的是( )
实数a,b在数轴上对应点的位置如图所示,下列各式中正确的是( )| A. | -a>b | B. | -a<b | C. | -a>-b | D. | a>-b |
 如图所示,在一条河的同岸有两个村庄A和B,两村要在河上合修一座桥,桥修在什么地方,可以使两个村庄到桥的距离之和最短?
如图所示,在一条河的同岸有两个村庄A和B,两村要在河上合修一座桥,桥修在什么地方,可以使两个村庄到桥的距离之和最短?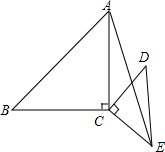 如图,AC=BC,DC=EC,且AC⊥BC,DC⊥EC.求证:
如图,AC=BC,DC=EC,且AC⊥BC,DC⊥EC.求证: