题目内容
3.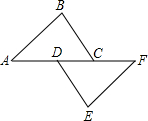 如图,在△ABC和△FED中,AD=FC,AB=FE,BC=ED,求证:
如图,在△ABC和△FED中,AD=FC,AB=FE,BC=ED,求证:(1)△ABC≌△FED;
(2)BC∥DE.
分析 (1)由AD=FC可得AC=DF,再根据SSS定理证明△ABC≌△FED;
(2)由△ABC≌△FED,得到∠BCA=∠EDF,于是证得结论.
解答 证明:(1)∵AD=CF,
∴AD+DC=CF+DC,
即AC=DF,
在△ABC和△FED中,
$\left\{\begin{array}{l}{AC=FD}\\{AB=EF}\\{CB=DE}\end{array}\right.$,
∴△ABC≌△FED;
(2)由(1)证得△ABC≌△FED,
∴∠BCA=∠EDF,
∴BC∥DE.
点评 本题考查三角形全等的判定方法,平行线的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
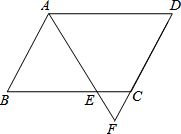 如图,在平行四边形ABCD中,E是BC边上的点,且BE=3EC,AE与DC的延长线交于点F.若CD=6,求CF的长.
如图,在平行四边形ABCD中,E是BC边上的点,且BE=3EC,AE与DC的延长线交于点F.若CD=6,求CF的长.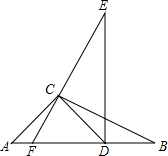 如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$.
如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$. 如图所示,在一条河的同岸有两个村庄A和B,两村要在河上合修一座桥,桥修在什么地方,可以使两个村庄到桥的距离之和最短?
如图所示,在一条河的同岸有两个村庄A和B,两村要在河上合修一座桥,桥修在什么地方,可以使两个村庄到桥的距离之和最短?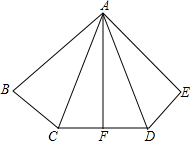 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.