Question

半径为2的⊙O中，弦AB⊥CD于E，且EO=1，则AB²+CD²的值为（　　）

• A、22
• B、24
• C、26
• D、28

Answer 1

考点：垂径定理,勾股定理

专题：

分析：画出图形，过O作ON⊥AB于N，OM⊥CD于M，连接OA，OD，得出矩形ONEM，推出ON=EM，EN=OM，求出OM²+ON²=OE²=1，由垂径定理得出AN=

1

2

AB，DM=

1

2

DC，由勾股定理求出4-

1

4

DC²+4-

1

4

AB²=1，即可求出答案．

解答：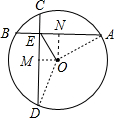
解：
过O作ON⊥AB于N，OM⊥CD于M，连接OA，OD，
∵AB⊥CD，
∴∠NEM=∠ENO=∠EMO=90°，
∴四边形NEMO是矩形，
∴ON=ME，OM=EN，
∵EN²+ON²=OE²=1，
∴OM²+ON²=OE²=1，
由垂径定理得：AN=

1

2

AB，DM=

1

2

DC，
∵由勾股定理得：OM²=OD²-DM²=2²-（

DC

2

）²，ON²=2²-（

AB

2

）²，
∴4-

1

4

DC²+4-

1

4

AB²=1，
即AB²+DC²=28，
故选D．

点评：本题考查了矩形的性质和判定，勾股定理，垂径定理等知识点，关键是构造直角三角形，能把已知条件和未知量联系起来．