题目内容
9. 如图,?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,求AB的长.
如图,?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,求AB的长.
分析 由?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,易证得△ABE,△CDE是等腰三角形,△BEC是直角三角形,则可求得BC的长,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠AEB=∠CBE,∠DEC=∠BCE,∠ABC+∠DCB=90°,
∵BE,CE分别是∠ABC和∠BCD的平分线,
∴∠ABE=∠CBE=$\frac{1}{2}$∠ABC,∠DCE=∠BCE=$\frac{1}{2}$∠DCB,
∴∠ABE=∠AEB,∠DCE=∠DEC,∠EBC+∠ECB=90°,
∴AB=AE,CD=DE,
∴AD=BC=2AB,
∵BE=4,CE=3,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=5,
∴AB=$\frac{1}{2}$BC=2.5.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及直角三角形的性质.注意证得△ABE,△CDE是等腰三角形,△BEC是直角三角形是关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
9.下列根式中,最简二次根式是( )
| A. | $\sqrt{25a}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{{a^2}+{b^2}}$ |
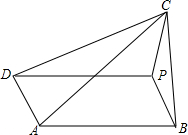 四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然.
四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然.
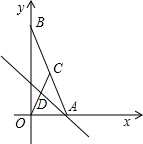 如图,在平面直角坐标系中,直线y=-2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.
如图,在平面直角坐标系中,直线y=-2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.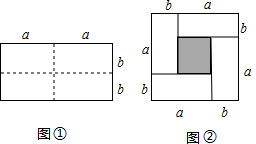 图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.