题目内容
12.请阅读下面的材料,并回答所提出的问题.三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
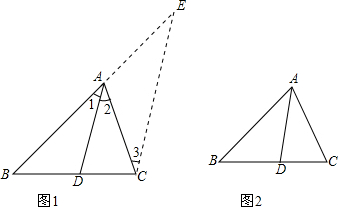
已知:如图1,△ABC中,AD是角平分线,求证:$\frac{BD}{DC}=\frac{AB}{AC}$
分析:要证$\frac{BD}{DC}=\frac{AB}{AC}$,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.
在比例式$\frac{BD}{DC}=\frac{AB}{AC}$中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明$\frac{BD}{DC}=\frac{AB}{AC}$就可以转化为证AE=AC.
(1)证明:过C作CE∥DA,交BA的延长线于E.(完成以下证明过程)
∴AE=AC(等腰三角形的判定定理)
∴△BAD∽△BEC,∴$\frac{BD}{BC}=\frac{AB}{BE}$(相似三角形的性质)∴$\frac{BD}{DC}=\frac{AB}{AC}$
(2)用三角形内角平分线性质定理解答问题:
已知:如图2,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.
求:BD的长.
分析 (1)对角平分线定理的证明:过C作CE∥DA,交BA的延长线于E,则根据平行线的性质得到∠1=∠E,∠2=∠3,加上∠1=∠2,则∠E=∠3,于是根据等腰三角形的判定定理得到AE=AC,再证明△BAD∽△BEC,根据相似的性质得$\frac{BD}{BC}$=$\frac{BA}{BE}$,然后用比例得性质易得$\frac{BD}{DC}=\frac{AB}{AC}$;
(2)根据角平分线定理得到$\frac{BD}{DC}=\frac{AB}{AC}$,即$\frac{BD}{7-BD}$=$\frac{5}{4}$,然后利用比例性质求解.
解答  (1)证明:∵CE∥DA,
(1)证明:∵CE∥DA,
∴∠1=∠E,∠2=∠3,
∵AD是角平分线,
∴∠1=∠2,
∴∠E=∠3,
∴AE=AC,
∵CE∥AD,
∴△BAD∽△BEC,
∴$\frac{BD}{BC}$=$\frac{BA}{BE}$,
∴$\frac{BD}{BC-BD}$=$\frac{BA}{BE-BA}$,
∴$\frac{BD}{DC}=\frac{AB}{AC}$;
故答案为等腰三角形的判定定理;相似三角形的性质;
(2)解:∵AD是角平分线,
∴$\frac{BD}{DC}=\frac{AB}{AC}$,即$\frac{BD}{7-BD}$=$\frac{5}{4}$,
∴BD=$\frac{35}{9}$(cm).
点评 本题考查了相似三角形的综合题:熟练掌握相似三角形的判定与性质,会利用相似比计算几何计算;本题证明了角平分线性质定理和此定理的运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
17. 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )| A. |  | B. |  | C. |  | D. | 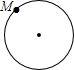 |
4.下列各式中是二次根式的是( )
| A. | $\sqrt{-7}$ | B. | $\root{3}{2m}$ | C. | $\sqrt{{x^2}+1}$ | D. | $\sqrt{a}$ |
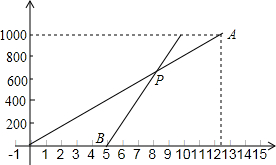 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题: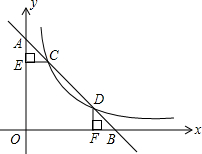 如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.
如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F. 如图,?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,求AB的长.
如图,?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,求AB的长.