Question

4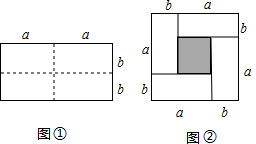．图①是一个长为2a，宽为2b的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．
（1）请用两种不同的方法求图2中阴影部分的面积：
方法1：（a+b）²-4ab；
方法2：（a-b）²；
（2）根据（1）的结果，请你写出（a+b）²、（a-b）²、ab之间的等量关系是（a+b）²-4ab=（a-b）²；
（3）根据（2）题中的等量关系，解决如下问题：a+b=$\sqrt{7}$，a-b=$\sqrt{2}$，求ab的值．

Answer 1

分析 （1）①从整体考虑，用大正方形的面积减去四个小矩形的面积就是阴影部分的面积；
②从局部考虑，根据正方形的面积公式，小正方形的边长的平方就是阴影部分的面积；
（2）根据所拼图形的面积相等，即可解答．
（3）把已知条件代入进行计算即可求解．

解答 解：（1）方法1：大正方形的面积减去四个小矩形的面积：（a+b）²-4ab，
方法2：阴影小正方形的面积：（a-b）²；
故答案为：：（a+b）²-4ab，（a-b）²；
（2）（a+b）²-4ab=（a-b）²；故答案为：（a+b）²-4ab=（a-b）²
（3）根据（2）的关系式，（a+b）²-4ab=（a-b）²，
∵a+b=$\sqrt{7}$，a-b=$\sqrt{2}$，
∴4ab=（a+b）²-$（a-b）^{2}=（\sqrt{7}）^{2}-（\sqrt{2}）^{2}$=5，
∴ab=$\frac{5}{4}$．

点评 本题考查了完全平方公式的几何背景，以及两个公式之间的关系，从整体与局部两种情况分析并写出面积的表达式是解题的关键．