题目内容
17.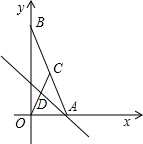 如图,在平面直角坐标系中,直线y=-2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.
如图,在平面直角坐标系中,直线y=-2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.(1)点C的坐标为(3,6);
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以为O、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
分析 (1)对于直线y=-2x+12,分别令x与y等于0,求出对应y与x的值,确定出A与B的坐标,得出线段AB的中点坐标,即为C的坐标;
(2)由C,D,以及OD=2CD,求出三等份点D坐标,设直线AD解析式为y=kx+b,把A与D坐标代入求出k与b的值,即可确定出直线AD解析式;
(3)在平面内存在点Q,使以为O、A、P、Q为顶点的四边形是菱形,如图所示,分三种情况考虑:当四边形OP1AQ1为菱形;当四边形OAP2Q2为菱形;当四边形AP3Q3O为菱形,分别求出Q坐标即可.
解答 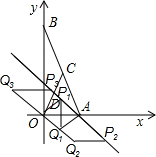 解:(1)对于直线y=-2x+12,
解:(1)对于直线y=-2x+12,
令x=0,得到y=12;令y=0,得到x=6,
∴A(6,0),B(0,12),
∵C为线段AB的中点,
∴C(3,6);
故答案为:(3,6);
(2)∵C(3,6),O(0,0),且OD=2CD,
∴D(2,4),
设直线AD解析式为y=kx+b,
把A与D坐标代入得:$\left\{\begin{array}{l}{6k+b=0}\\{2k+b=4}\end{array}\right.$,
解得:k=-1,b=6,
∴直线AD解析式为y=-x+6;
(3)在平面内存在点Q,使以为O、A、P、Q为顶点的四边形是菱形,
如图所示,分三种情况考虑:
当四边形OP1AQ1为菱形,由A(6,0)及菱形性质得到P1与Q1横坐标为3,
把x=3代入直线y=-x+6,得:y=3,即P1(3,3),Q1(3,-3);
当四边形OAP2Q2为菱形,可得AP2=OA=6,设P2(x,-x+6),
根据勾股定理得:(x-6)2+(-x+6)2=62,
解得:x=6+3$\sqrt{2}$或x=6-3$\sqrt{2}$(舍去),
此时P2(6+3$\sqrt{2}$,-3$\sqrt{2}$),Q2(3$\sqrt{2}$,-3$\sqrt{2}$);
当四边形AP3Q3O为菱形,可得OQ3=OA=6,设P3(a,-a+6),Q3(a-6,-a+6),
根据勾股定理得:(a-6)2+(-a+6)2=62,
解得:a=6+3$\sqrt{2}$(舍去)或a=6-3$\sqrt{2}$,
此时P3(6-3$\sqrt{2}$,3$\sqrt{2}$),Q3(-3$\sqrt{2}$,3$\sqrt{2}$),
综上,在平面内存在点Q,使以为O、A、P、Q为顶点的四边形是菱形,此时Q坐标为(3,-3)或(3$\sqrt{2}$,-3$\sqrt{2}$)或(-3$\sqrt{2}$,3$\sqrt{2}$).
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,待定系数法确定一次函数解析式,坐标与图形性质,菱形的性质,利用了分类讨论的思想,熟练掌握待定系数法是解本题第二问的关键.

| 业务种类 | 计费单位 | 资费标准/元 | |
| 本埠资费 | 外埠资费 | ||
| 信函 | 首重100克内,每重20克(不足20克按20克计算) | 0.80 | 1.20 |
| 续重101-2000克每重100克(不足100克按100克计算) | 1.20 | 2.00 | |
(2)如果邮寄100g以上400g以内的邮件,最多贴4张邮票,要邮寄145g的邮件往本市,只用80分、1.2元和2元的邮票,选择哪几张邮票来贴?
(3)一个250g的邮件如果寄往外省,只用80分、1.2元和4元的邮票,选哪几张邮票支付邮资刚好?
(1)长度相等的两条弧是等弧;
(2)半径相等的两个半圆是等弧;
(3)同圆中,优弧与劣弧的和等于一个整圆;
(4)分别在两个等圆上两条弧是等弧;
(5)能够完全重合的弧是等弧.
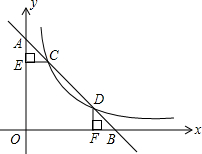 如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.
如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F. 如图,?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,求AB的长.
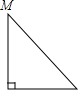
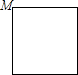
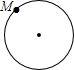
如图,?ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,求AB的长. 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )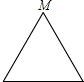
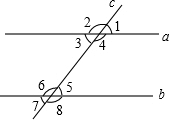 如图所示,直线a,b被直线c所截,现给出下列四个条件①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7,其中能判定a∥b的条件序号是( )
如图所示,直线a,b被直线c所截,现给出下列四个条件①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7,其中能判定a∥b的条件序号是( )