题目内容
已知二次函数y=x2-2(m+1)x+m(m+2)
(1)求证:无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值.
(2)若该函数图象的对称轴为直线x=2,试求二次函数的最小值.
(1)求证:无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值.
(2)若该函数图象的对称轴为直线x=2,试求二次函数的最小值.
考点:抛物线与x轴的交点,二次函数的最值
专题:计算题
分析:(1)设抛物线与x轴的两交点分别为(a,0),(b,0),根据抛物线与x轴的交点问题,得到方程x2-2(m+1)x+m(m+2)=0的两根分别为a与b,根据根与系数的关系得a+b=2(m+1),ab=m(m+2),而函数图象与x轴两个交点之间的距离可表示为|a-b|,然后根据代数式的变形得到|a-b|=
=
,再利用整体代入的方法得到|a-b|=
=2,由此可判断函数图象与x轴两个交点之间的距离为定值.
(2)根据抛物线的对称轴方程得到x=-
=2,解得m=0,则抛物线解析式为y=x2-2x,然后配成顶点式得到二次函数的最小值.
| (a-b)2 |
| (a+b)2-4ab |
| 4(m+1)2-4m(m+2) |
(2)根据抛物线的对称轴方程得到x=-
| -2(m+1) |
| 1 |
解答:(1)证明:设抛物线与x轴的两交点分别为(a,0),(b,0),
则a+b=2(m+1),ab=m(m+2),
所以|a-b|=
=
=
=2,
即无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值;
(2)解:根据题意得x=-
=2,解得m=0,
则抛物线解析式为y=x2-2x=(x-1)2-1,
所以二次函数的最小值为-1.
则a+b=2(m+1),ab=m(m+2),
所以|a-b|=
| (a-b)2 |
| (a+b)2-4ab |
| 4(m+1)2-4m(m+2) |
即无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值;
(2)解:根据题意得x=-
| -2(m+1) |
| 1 |
则抛物线解析式为y=x2-2x=(x-1)2-1,
所以二次函数的最小值为-1.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了二次函数的性质.

练习册系列答案
相关题目
 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.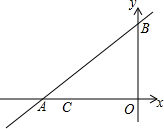 如图,直线y=
如图,直线y=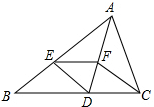 如图,△ABC中,AD平分∠BAC交BC于点D,在线段AB上截取AE=AC,过点E作EF∥BC交AD于点F.
如图,△ABC中,AD平分∠BAC交BC于点D,在线段AB上截取AE=AC,过点E作EF∥BC交AD于点F.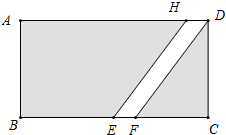 如图,在宽为40m的一条绿化带上开一条路,若EF=10m,FC=30m,则这条路的宽度为多少m?
如图,在宽为40m的一条绿化带上开一条路,若EF=10m,FC=30m,则这条路的宽度为多少m?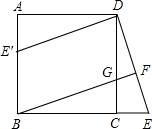 如图所示,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接
如图所示,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接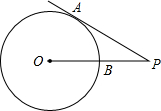 如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为
如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为