题目内容
如图，已知正方形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，抛物线y=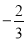
x2+bx+c经过点A，B，交正x轴于点D，E是OC上的动点（不与C重合）连接EB，过B点作BF⊥BE交y轴与F
（1）求b，c的值及D点的坐标；
（2）求点E在OC上运动时，四边形OEBF的面积有怎样的规律性？并证明你的结论；
（3）连接EF，BD，设OE=m，△BEF与△BED的面积之差为S，问：当m为何值时S最小，并求出这个最小值．
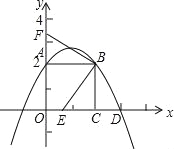
（1）b=，c=2；D点坐标为（3，0）．（2）点E在OC上运动时，四边形OEBF的面积不变；（3）当m=2﹣时S最小为0．
【解析】
试题分析：（1）把点A，B代入抛物线y=x2+bx+c求得b、c即可，y=0，建立方程求得点D；
（2）四边形OEBF的面积不变，利用三角形全等证得结论即可；
（3）用m分别表示出两个三角形的面积，求差探讨得出答案即可．
试题解析：（...
名校课堂系列答案若抛物线y=x2+bx+c与x轴只有一个交点，且过点A（m，n），B（m+6，n），则n= ．
9
【解析】
分析：∵抛物线y=x2+bx+cx轴只有一个交点，∴当时，y=0．且b2﹣4c=0，即b2=4c．
又∵点A（m，n），B（m+6，n），∴点A、B关于直线对称。
∴A（，n），B（，n）。
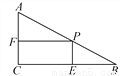
将A点坐标代入抛物线解析式，得：。 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝12cm，点P是AB边上的一个动点，过点P作PE⊥BC，PF⊥AC.当PB＝_________时，四边形PECF的面积最大，最大值为_______．
6cm 9cm2
【解析】利用锐角三角函数关系，设PB=xcm，由∠C=90°，∠B=30°，AB=12cm，可得BC=AB×cos30°=6（cm），PE=xcm，BE=xcm，则EC=（6-x）cm，故四边形FCEP的面积为：PE×EC=x×（6-x）=-x2+3x=-（x2-12x）=-（x-6）2+9，故当x=6时，四边形PECF的面积最大，最大值为9．
故答案为：6，9． 关于这一图案，下列说法正确的是（ ）
A. 图案乙是由甲绕BC的中点旋转180°得到的
B. 图案乙是由甲绕点C旋转108°得到的
C. 图案乙是由甲沿AB方向平移3个边长的距离得到的
D. 图案乙是由甲沿直线BC翻转180°得到的
A
【解析】【解析】
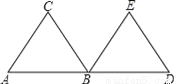
如图所示：可得图案乙是由甲绕BC的中点旋转180°得到的．故选A． 如图，△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．由一个三角形变换到另一个三角形（ ）
A. 仅能由平移得到
B. 仅能由旋转得到
C. 既能由平移得到，也能由旋转得到
D. 既不能由平移得到，也不能由旋转得到
C
【解析】【解析】
∵△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．
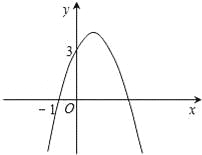
∴这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的．故选C． 已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）．
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围．
（1）b="2,c=3," y=﹣x2+2x+3．(2) ﹣1＜x＜3
【解析】试题分析：（1）把抛物线上的两点代入解析式，解方程组可求b、c的值；
（2）令y=0，求抛物线与x轴的两交点坐标，观察图象，求y＞0时，x的取值范围．
试题解析：（1）将点（﹣1，0），（0，3）代入y=﹣x2+bx+c中，得
，解得．
∴y=﹣x2+2x+3．
（2）令y=0，解方... 已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
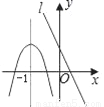
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
D
【解析】解析：对称轴为直线x=﹣1，且﹣1＜x1＜x2，当x＞﹣1时，y2＜y1，
又因为x3＜﹣1，由一次函数的图象可知，此时点P3（x3，y3）在二次函数图象上方，
所以y2＜y1＜y3．
故选：D． 如图，已知DE∥BC，AB=AC，∠1=125°，则∠C的度数是（ ）
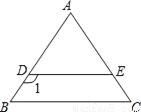
A. 55° B. 45° C. 35° D. 65°
A
【解析】∵∠1=125°，DE∥BC，∴∠B=180°–125°=55°，∵AB=AC，∴∠C=∠B=55°，故选A． 分解因式：16－x2＝( )
A. (4－x)(4＋x) B. (x－4)(x＋4)
C. (8＋x)(8－x) D. (4－x)2
A
【解析】试题分析：直接利用平方差公式分解因式得出答案．16﹣x2=（4﹣x）（4+x）．