题目内容
分解因式：16－x2＝( )
A. (4－x)(4＋x) B. (x－4)(x＋4)
C. (8＋x)(8－x) D. (4－x)2
A
【解析】试题分析：直接利用平方差公式分解因式得出答案．16﹣x2=（4﹣x）（4+x）．
练习册系列答案
相关题目
如图，已知正方形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，抛物线y=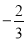
x2+bx+c经过点A，B，交正x轴于点D，E是OC上的动点（不与C重合）连接EB，过B点作BF⊥BE交y轴与F
（1）求b，c的值及D点的坐标；
（2）求点E在OC上运动时，四边形OEBF的面积有怎样的规律性？并证明你的结论；
（3）连接EF，BD，设OE=m，△BEF与△BED的面积之差为S，问：当m为何值时S最小，并求出这个最小值．
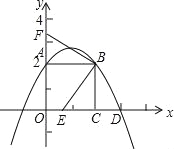
（1）b=，c=2；D点坐标为（3，0）．（2）点E在OC上运动时，四边形OEBF的面积不变；（3）当m=2﹣时S最小为0．
【解析】
试题分析：（1）把点A，B代入抛物线y=x2+bx+c求得b、c即可，y=0，建立方程求得点D；
（2）四边形OEBF的面积不变，利用三角形全等证得结论即可；
（3）用m分别表示出两个三角形的面积，求差探讨得出答案即可．
试题解析：（... 如图，△ABC中，∠C＝90°，CD⊥AB，CM平分AB，CE平分∠DCM，则∠ACE的度数是______．
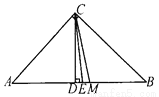
45°
【解析】∵△ABC中,∠C=90°，
∴∠A+∠B=90°，
∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠ACD=∠B，
∵CM平分AB，
∴AM=BM=CM，
∴∠BCM=∠B，
∴∠BCM=∠ACD，
∵CE平分∠DCM，
∴∠DCE=∠MCE，
∴∠ACD+∠DCE=∠BCM+∠M... 一个钝角三角形的三条角平分线所在的直线一定交于一点，这交点一定在( )
A. 三角形内部 B. 三角形的一边上 C. 三角形外部 D. 三角形的某个顶点上
A
【解析】三角形三条角平分线所在的直线一定交于一点，这一点是三角形的内心即内切圆的圆心，此点在三角形（锐角三角形、直角三角形、钝角三角形）内部.
故选：A. 已知|x﹣y+2|+
=0，则x2﹣y2的值为______．
﹣4
【解析】因为|x?y+2|+=0，∴x?y+2=0，x+y?2=0，
∴x?y=?2，x+y=2，∴x²?y²=(x?y)(x+y)=?4.
故答案为：?4. 二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：
（1）一次函数和二次函数的解析式；
（2）写出使一次函数值大于二次函数值的x的取值范围．
（1）y1=﹣x2﹣2x+3（2）x＜﹣2或x＞1．
【解析】
试题分析：（1）将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式，进而可根据抛物线的对称轴求出D点的坐标，再用待定系数法求出一次函数解析式；
（2）根据（1）画出函数图象，即可写出一次函数值大于二次函数值的x的取值范围．
【解析】
（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），... 已知抛物线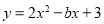
的对称轴是直线
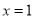，则
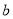的值为 ．
b=4
【解析】
试题分析：由抛物线的对称轴x=-和已知条件抛物线y=2-bx+3的对称轴是直线x=1，得到的等式，即可求出b的值． 已知抛物线y=ax2+bx+3的对称轴是直线x=1．
（1）求证：2a+b=0；
（2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．
（1）见解析；（2）x=－2
【解析】试题分析：直接利用对称轴公式代入求出即可；根据（1）中所求，再将x=4代入方程求出a，b的值，进而解方程得出即可．
试题解析：（1）证明：∵对称轴是直线x=1=﹣，∴b=－2a ∴2a+b=0；
（2）∵ax2+bx﹣8=0的一个根为4，∴16a+4b﹣8=0，∵b=﹣2a，∴16a﹣8a﹣8=0，
解得：a=1，则b=﹣2，∴a+bx... 在□ABCD中，∠A+∠C=270°，则∠B=______，∠C=______.
45° 135°
【解析】【解析】
∵已知平行四边形ABCD，∴∠A=∠C，∠B+∠C=180°．
又∵∠A+∠C=270°，∴2∠C=270°，∠C=135°，∴∠B=180°-∠C=180°-135°=45°．
故答案为：∠C=135°，∠B=45°．