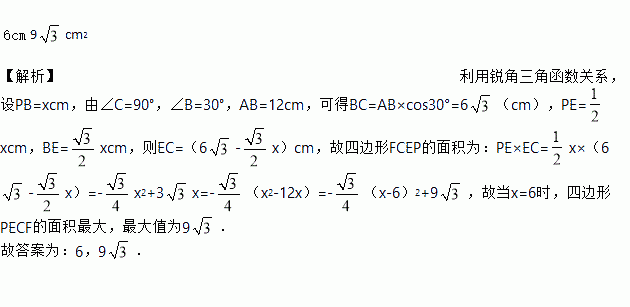题目内容
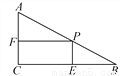
如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝12cm，点P是AB边上的一个动点，过点P作PE⊥BC，PF⊥AC.当PB＝_________时，四边形PECF的面积最大，最大值为_______．
6cm 9cm2
【解析】利用锐角三角函数关系，设PB=xcm，由∠C=90°，∠B=30°，AB=12cm，可得BC=AB×cos30°=6（cm），PE=xcm，BE=xcm，则EC=（6-x）cm，故四边形FCEP的面积为：PE×EC=x×（6-x）=-x2+3x=-（x2-12x）=-（x-6）2+9，故当x=6时，四边形PECF的面积最大，最大值为9．
故答案为：6，9．
阅读快车系列答案小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）
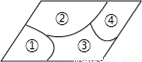
A. ①，② B. ①，④ C. ③，④ D. ②，③
D
【解析】分析：本题考查的是平行四边形的性质.
解析：破碎的玻璃中的②和③是连接的，可以得到四边形的大小.
故选B. 世界杯决赛分成8个小组，每小组4个队，小组进行单循环（每个队都与该小组的其他队比赛一场）比赛，选出2个队进入16强，胜一场得3分，平一场得1分，负一场得0分．
（1）求每小组共比赛多少场？
（2）在小组比赛中，现有一队得到6分，该队出线是一个确定事件，还是不确定事件？
（1）6；（2）该队出线是一个不确定事件；
【解析】试题分析：（1）利用单循环的方法进行计算即可．
（2）根据必然事件、不可能事件、随机事件的概念可区别各类事件．
试题解析：（1）4×3÷2 =6（场）
答：每小组共比赛6场。
（2）因为总共有6场比赛，每场比赛最多可得3分，则6场比赛最多共有3×6=18分，现有一队得6分，还剩下12分，则还有可能有2个队同时得6分，... 下列事件中，属于必然事件的是（ ）
A. 打开电视，正在播放《新闻联播》 B. 抛掷一次硬币正面朝上
C. 袋中有3个红球，从中摸出一球是红球 D. 阴天一定下雨
C
【解析】试题解析：A．打开电视，正在播放《新闻联播》是随机事件，因为也可能播放其它内容；
B．抛掷一次硬币正面朝上是随机事件，也可能反面朝上；
C. 袋中有3个红球，从中摸出一球是红球，是必然事件，因为袋子中只有红球，无论怎么摸，只能摸出红球；
D．阴天一定下雨是随机事件，也可能只阴天不下雨.
故选C. 某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形．其中，抽屉底面周长为180cm，高为20cm．请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？（材质及其厚度等暂忽略不计）．
当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3
【解析】【解析】
已知抽屉底面宽为x cm，则底面长为180÷2－x=（90－x）cm．
由题意得：。
∴当x=45时，y有最大值，最大值为40500。
答：当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3。
根据题意列出二次函数关系式，然后利用二次函数的性质求最大值。
... 如图，在平面直角坐标系中，四边形OBCD是边长为4的正方形，平行于对角线BD的直线l从O出发，沿x轴正方向以每秒1个单位长度的速度运动，运动到直线l与正方形没有交点为止．设直线l扫过正方形OBCD的面积为S，直线l运动的时间为t(秒)，下列能反映S与t之间函数关系的图象是( )
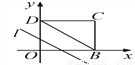
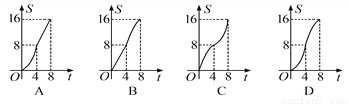
A. A B. B C. C D. D
D
【解析】试题分析：根据三角形的面积即可求出S与t的函数关系式，根据函数关系式选择图象．
试题解析：如图：
①当0≤t≤4时，S=×t×t=t2，即S=t2．
该函数图象是开口向上的抛物线的一部分．
故B、C错误；
②当4＜t≤8时，S=16-×（8-t）×（8-t）=-t2+8t-16．
该函数图象是开口向下的抛物线的一部分．
故A错误．
... 如图,如果将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中四边形ACED的面积为_____.
15
【解析】试题分析：：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
试题解析：设点A到BC的距离为h，则S△ABC=BC•h=5，
∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×5=15... 如图，已知正方形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，抛物线y=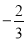
x2+bx+c经过点A，B，交正x轴于点D，E是OC上的动点（不与C重合）连接EB，过B点作BF⊥BE交y轴与F
（1）求b，c的值及D点的坐标；
（2）求点E在OC上运动时，四边形OEBF的面积有怎样的规律性？并证明你的结论；
（3）连接EF，BD，设OE=m，△BEF与△BED的面积之差为S，问：当m为何值时S最小，并求出这个最小值．
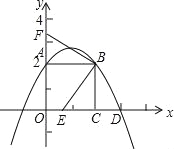
（1）b=，c=2；D点坐标为（3，0）．（2）点E在OC上运动时，四边形OEBF的面积不变；（3）当m=2﹣时S最小为0．
【解析】
试题分析：（1）把点A，B代入抛物线y=x2+bx+c求得b、c即可，y=0，建立方程求得点D；
（2）四边形OEBF的面积不变，利用三角形全等证得结论即可；
（3）用m分别表示出两个三角形的面积，求差探讨得出答案即可．
试题解析：（... 如图，△ABC中，∠C＝90°，CD⊥AB，CM平分AB，CE平分∠DCM，则∠ACE的度数是______．
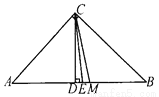
45°
【解析】∵△ABC中,∠C=90°，
∴∠A+∠B=90°，
∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠ACD=∠B，
∵CM平分AB，
∴AM=BM=CM，
∴∠BCM=∠B，
∴∠BCM=∠ACD，
∵CE平分∠DCM，
∴∠DCE=∠MCE，
∴∠ACD+∠DCE=∠BCM+∠M...