题目内容
若抛物线y=x2+bx+c与x轴只有一个交点，且过点A（m，n），B（m+6，n），则n= ．
9
【解析】
分析：∵抛物线y=x2+bx+cx轴只有一个交点，∴当时，y=0．且b2﹣4c=0，即b2=4c．
又∵点A（m，n），B（m+6，n），∴点A、B关于直线对称。
∴A（，n），B（，n）。
将A点坐标代入抛物线解析式，得：。
如图，在△ABC中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于 cm．
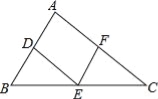
14.
【解析】
试题分析：∵D、E分别AB、BC的中点，∴AD=AB，DE=AC.同理AF=AC，EF=AB.∴l四边形ADEF=AD+DE+EF+AF=（AB+AC+AB+AC）=AB+AC=14cm. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）
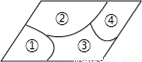
A. ①，② B. ①，④ C. ③，④ D. ②，③
D
【解析】分析：本题考查的是平行四边形的性质.
解析：破碎的玻璃中的②和③是连接的，可以得到四边形的大小.
故选B. 抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线于x轴的一个交点坐标为（﹣2，0）
B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
C
【解析】【解析】
当x=﹣2时，y=0，∴抛物线过（﹣2，0），∴抛物线与x轴的一个交点坐标为（﹣2，0），故A正确；
当x=0时，y=6，∴抛物线与y轴的交点坐标为（0，6），故B正确；
当x=0和x=1时，y=6，∴对称轴为x=，故C错误；
当x＜时，y随x的增大而增大，∴抛物线在对称轴左侧部分是上升的，故D正确；
故选C． 在下列y关于x的函数中，一定是二次函数的是（ ）
A. y=2x2 B. y=2x﹣2 C. y=ax2 D.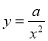 
A
【解析】解：A．是二次函数，故A符合题意；
B．是一次函数，故B错误；
C．a=0时，不是二次函数，故C错误；
D．a≠0时是分式方程，故D错误；
故选A． 如图，二次函数y＝ax2＋bx＋c(a≠0)的图象的顶点在第一象限，且过点(0，1)和(－1，0)．下列结论：①ab＜0；②b2＞4a；③0＜a＋b＋c＜2；④0＜b＜1；⑤当x＞－1时，y＞0.其中正确结论的个数是( )
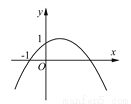
A. 5个 B. 4个 C. 3个 D. 2个
B
【解析】由抛物线的对称轴x=-在y轴右侧，可以判定a、b异号，由此确定①正确；
由抛物线与x轴有两个交点得到b2-4ac＞0，又抛物线过点（0，1），得出c=1，由此判定②正确；
由a-b+c=0，及b＞0得出a+b+c=2b＞0；由b＜1，c=1，a＜0，得出a+b+c＜a+1+1＜2，由此判定③正确；
由抛物线过点（-1，0），得出a-b+c=0，即a=b-1，由a＜0得出... 世界杯决赛分成8个小组，每小组4个队，小组进行单循环（每个队都与该小组的其他队比赛一场）比赛，选出2个队进入16强，胜一场得3分，平一场得1分，负一场得0分．
（1）求每小组共比赛多少场？
（2）在小组比赛中，现有一队得到6分，该队出线是一个确定事件，还是不确定事件？
（1）6；（2）该队出线是一个不确定事件；
【解析】试题分析：（1）利用单循环的方法进行计算即可．
（2）根据必然事件、不可能事件、随机事件的概念可区别各类事件．
试题解析：（1）4×3÷2 =6（场）
答：每小组共比赛6场。
（2）因为总共有6场比赛，每场比赛最多可得3分，则6场比赛最多共有3×6=18分，现有一队得6分，还剩下12分，则还有可能有2个队同时得6分，... 下列事件中，属于必然事件的是（ ）
A. 打开电视，正在播放《新闻联播》 B. 抛掷一次硬币正面朝上
C. 袋中有3个红球，从中摸出一球是红球 D. 阴天一定下雨
C
【解析】试题解析：A．打开电视，正在播放《新闻联播》是随机事件，因为也可能播放其它内容；
B．抛掷一次硬币正面朝上是随机事件，也可能反面朝上；
C. 袋中有3个红球，从中摸出一球是红球，是必然事件，因为袋子中只有红球，无论怎么摸，只能摸出红球；
D．阴天一定下雨是随机事件，也可能只阴天不下雨.
故选C. 如图，已知正方形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，抛物线y=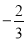
x2+bx+c经过点A，B，交正x轴于点D，E是OC上的动点（不与C重合）连接EB，过B点作BF⊥BE交y轴与F
（1）求b，c的值及D点的坐标；
（2）求点E在OC上运动时，四边形OEBF的面积有怎样的规律性？并证明你的结论；
（3）连接EF，BD，设OE=m，△BEF与△BED的面积之差为S，问：当m为何值时S最小，并求出这个最小值．
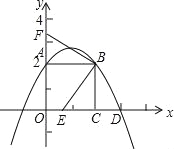
（1）b=，c=2；D点坐标为（3，0）．（2）点E在OC上运动时，四边形OEBF的面积不变；（3）当m=2﹣时S最小为0．
【解析】
试题分析：（1）把点A，B代入抛物线y=x2+bx+c求得b、c即可，y=0，建立方程求得点D；
（2）四边形OEBF的面积不变，利用三角形全等证得结论即可；
（3）用m分别表示出两个三角形的面积，求差探讨得出答案即可．
试题解析：（...