题目内容
19. 如图所示直角梯形的中位线长为a,一腰长为b,此腰与下底所成的夹角为30°,则梯形的面积的表达式为( )
如图所示直角梯形的中位线长为a,一腰长为b,此腰与下底所成的夹角为30°,则梯形的面积的表达式为( )| A. | $\frac{1}{2}$ab | B. | $\frac{1}{3}$ab | C. | $\frac{1}{4}$ab | D. | ab |
分析 根据梯形的面积等于梯形的中位线×高,则只需求得梯形的高;根据30°的直角三角形的性质即可求解.
解答 解:∵一腰长为b,这个腰与底边所成的角为30°,
∴梯形的高为$\frac{1}{2}$b.
∴它的面积为$\frac{1}{2}$×2a×$\frac{1}{2}$b=$\frac{1}{2}$ab.
故选A.
点评 本题考查了梯形的中位线定理,综合运用了梯形的面积公式以及30°的直角三角形的性质是解题的关键.

练习册系列答案
相关题目
14. 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )| A. | y=6-$\frac{1}{2}$x(0<x<12) | B. | y=-$\frac{1}{2}$x2+6x(0<x<12) | ||
| C. | y=2x2-12x(0<x<12) | D. | y=$\frac{1}{2}$x2+6x(0<x<12) |
11.因式分解的结果是(x+y-z)(x-y+z)的多项式是( )
| A. | x2-(y+z)2 | B. | (x-y)2-z2 | C. | -(x-y)2+z2 | D. | x2-(y-z)2 |
8. 在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
 在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )| A. | ${(\frac{1}{2})}^{2015}$ | B. | ${(\frac{1}{2})}^{2016}$ | C. | ${(\frac{\sqrt{3}}{3})}^{2015}$ | D. | ${(\frac{\sqrt{3}}{3})}^{2016}$ |
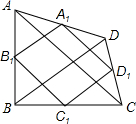 如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为9cm.
如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为9cm. 如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点. 如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC.
如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC. 如图,在矩形ABCD中,有以下结论:
如图,在矩形ABCD中,有以下结论: 已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.
已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.