题目内容
12.若一个角的余角是这个角的$\frac{1}{4}$,则这个角是72°,这个角的补角是108°.分析 设这个角为x°,根据题意得出$\frac{1}{4}$x=90-x,求出x的值,再根据补角定义得出即可.
解答 解:设这个角为x°,根据题意得:
$\frac{1}{4}$x=90-x,
解得:x=72,
即这个角为72°,
则这个角的补角为180°-72°=108°.
故答案为:72°,108°.
点评 本题考查了余角,补角的应用,解此题的关键是能根据题意求出这个角的度数,注意:∠A的余角为90°-∠A,∠A的补角为180°-∠A.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
2.把方程$\frac{0.2x-1}{0.3}$-2=$\frac{0.1x-0.7}{0.5}$的分母化为整数的方程是( )
| A. | $\frac{2x-10}{3}$-20=$\frac{x-7}{5}$ | B. | $\frac{2x-10}{3}$-2=$\frac{x-7}{5}$ | C. | $\frac{2x-1}{3}$-2=$\frac{x-7}{5}$ | D. | $\frac{2x-1}{3}$-20=$\frac{x-7}{5}$ |
3.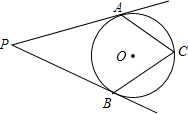 如图,PA,PB是⊙O的切线,切点分别为A,B,C在⊙O上,则∠P与∠C的关系是( )
如图,PA,PB是⊙O的切线,切点分别为A,B,C在⊙O上,则∠P与∠C的关系是( )
 如图,PA,PB是⊙O的切线,切点分别为A,B,C在⊙O上,则∠P与∠C的关系是( )
如图,PA,PB是⊙O的切线,切点分别为A,B,C在⊙O上,则∠P与∠C的关系是( )| A. | 2∠P+∠C=180° | B. | 2∠P+∠C=360° | C. | ∠P+2∠C=180° | D. | ∠P+∠C=180° |
4.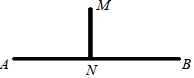 如图所示,把河水引向水池M,要向水池M点向河岸AB画垂线,垂足为N,再沿垂线MN开一条渠道才能使渠道最短.其依据是( )
如图所示,把河水引向水池M,要向水池M点向河岸AB画垂线,垂足为N,再沿垂线MN开一条渠道才能使渠道最短.其依据是( )
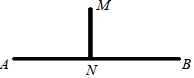 如图所示,把河水引向水池M,要向水池M点向河岸AB画垂线,垂足为N,再沿垂线MN开一条渠道才能使渠道最短.其依据是( )
如图所示,把河水引向水池M,要向水池M点向河岸AB画垂线,垂足为N,再沿垂线MN开一条渠道才能使渠道最短.其依据是( )| A. | 垂线段最短 | |
| B. | 过一点确定一条直线与已知直线垂直 | |
| C. | 两点之间线段最短 | |
| D. | 以上说法都不对 |
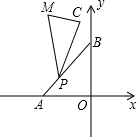 如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度.
如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度. 如图所示是某台阶的一部分,如果点A的坐标为(0,0),B点的坐标为(1,1).
如图所示是某台阶的一部分,如果点A的坐标为(0,0),B点的坐标为(1,1).