题目内容
3．
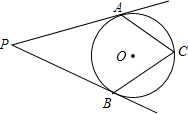如图，PA，PB是⊙O的切线，切点分别为A，B，C在⊙O上，则∠P与∠C的关系是（ ）| A． | 2∠P+∠C=180° | B． | 2∠P+∠C=360° | C． | ∠P+2∠C=180° | D． | ∠P+∠C=180° |
分析 连接OA、OB．根据切线的性质，得到∠OAP=∠OBP=90°，根据四边形的内角和定理即可求得∠P+∠AOB=180°，再进一步根据圆周角定理求解即可．
解答 解：连接OA、OB．
∵PA、PB是⊙O的切线，切点分别为A、B，
∴∠OAP=∠OBP=90°（切线的性质），
∴∠P+∠AOB=180°，
∵∠C=$\frac{1}{2}$∠AOB，
∴∠P+2∠C=180°．
故选：C．
点评 此题主要考查了切线的性质定理、四边形的内角和定理以及圆周角定理．连接OA与OB，熟练运用性质及定理是解本题的关键．
练习册系列答案
相关题目
如图，直线y=x+b与直线y=kx+6交于点P（3，5），则关于x的不等式kx+6＞x+b的解集是x＜3．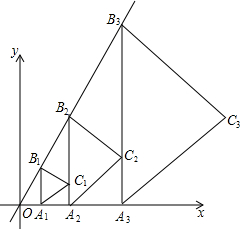
如图，点A1（1，0）在x轴上，过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1，以A1B1为边在A1B1的右侧作等边△A1B1C1，再过点C1作A2B2∥y轴，分别交直线x轴和直线y=$\sqrt{3}$x于A2，B2两点，再以A2B2为边在A2B2的右侧作等边△A2B2C2…，按此规律进行下去，则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$（\frac{5}{2}）^{n-1}$•$\sqrt{3}$]2（用含正整数n的代数式表示）．
18．用公式法解方程3x2+4=12x，下列代入公式正确的是（ ）
| A． | x=$\frac{12±\sqrt{1{2}^{2}-3×4}}{2}$ | B． | x=$\frac{-12±\sqrt{1{2}^{2}-3×4}}{2}$ | ||
| C． | x=$\frac{12±\sqrt{1{2}^{2}+3×4}}{2}$ | D． | x=$\frac{-（-12）±\sqrt{（-12）^{2}-4×3×4}}{2×3}$ |
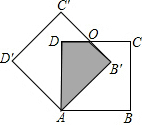如图，边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′，则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$．