题目内容
13.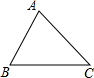 如图,△ABC是锐角三角形,sinC=$\frac{4}{5}$,则sinA的取值范围是( )
如图,△ABC是锐角三角形,sinC=$\frac{4}{5}$,则sinA的取值范围是( )| A. | 0$<sinA<\frac{3}{5}$ | B. | $\frac{4}{5}<sinA<1$ | C. | $\frac{3}{5}<sinA<\frac{4}{5}$ | D. | $\frac{3}{5}<sinA<1$ |
分析 作AH⊥BC于H,如图,根据正弦定义得到sinC=$\frac{AH}{AC}$=$\frac{4}{5}$,则可设AH=4x,AC=5x,利用勾股定理得到CH=3x,所以sin∠HAC=$\frac{HC}{AC}$=$\frac{3}{5}$,由于∠HAC<∠BAC<90°,然后根据正弦函数为增函数即可得到sin∠BAC的范围.
解答 解:作AH⊥BC于H,如图,
在Rt△ACH中,sinC=$\frac{AH}{AC}$=$\frac{4}{5}$,
设AH=4x,AC=5x,
所以CH=$\sqrt{(5x)^{2}-(4x)^{2}}$=3x,
所以sin∠HAC=$\frac{HC}{AC}$=$\frac{3}{5}$,
∵∠HAC<∠BAC<90°,
∴$\frac{3}{5}$<sin∠BAC<1.
故选D.
点评 本题考查了锐角三角函数的增减性:锐角三角函数值都是正值;当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大);当角度在0°≤∠A≤90°间变化时,0≤sinA≤1,1≥cosA≥0.

练习册系列答案
相关题目
1.已知(x+a)(x+b)=x2-13x+36,则a+b=( )
| A. | -5 | B. | 5 | C. | -13 | D. | -13或5 |
3.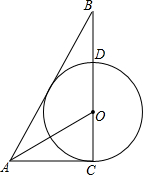 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}$π | D. | $\frac{16}{9}$π |