题目内容
已知:△ABC内接于⊙O,AB=AC,D是
一点,E是DB延长线上一点,AE=AD.
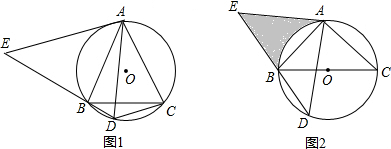
(1)如图1,求证:BE=CD;
(2)如图2,若AB=2,∠BAC=90°,
=
,求阴影部分的面积.
 |
| BC |
(1)如图1,求证:BE=CD;
(2)如图2,若AB=2,∠BAC=90°,
 |
| BD |
| 1 |
| 2 |
 |
| CD |

考点:圆周角定理,全等三角形的判定与性质,扇形面积的计算
专题:证明题
分析:(1)通过证明△ABE≌△ACD得到BE=CD;
(2)连结OA、CD,作BH⊥AE于H,如图,先求出∠E=45°,∠EAD=90°,∠EAB=60°,在Rt△HAB中利用含30度的直角三角形三边的关系计算出AH=
AB=1,BH=
AH=
,在Rt△BHE中得到EH=BH=
,
则可计算出S△ABE=
,接着计算出S弓形AB=S扇形AOB-S△AOB=
π-1,然后用△ABE的面积减去弓形AB的面积即可得到阴影部分的面积.
(2)连结OA、CD,作BH⊥AE于H,如图,先求出∠E=45°,∠EAD=90°,∠EAB=60°,在Rt△HAB中利用含30度的直角三角形三边的关系计算出AH=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
则可计算出S△ABE=
| ||
| 2 |
| 1 |
| 2 |
解答:(1)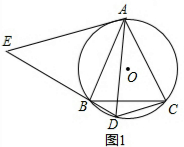 证明:∵AE=AD,
证明:∵AE=AD,
∴∠E=∠ADE,
∵AB=AC,
∴∠ADE=∠ADC,
∴∠E=∠ADC,
∵∠ABE为圆内接四边形ABDC的外角,
∴∠ABE=∠ACD,
在△ABE和△ACD中,
,
△ABE≌△ACD,
∴BE=CD;
(2)连结OA、CD,作BH⊥AE于H,如图,
∵∠BAC=90°,AB=AC,
∴BC为直径,∠ABC=∠ACB=45°,
∴∠BDC=90°,
∵
=
,
∴∠DBC=2∠BCD,
∴∠DBC=60°,∠BCD=30°,
∴∠BAD=∠BCD=30°,
∵∠ADE=∠ACB=45°,
∵AE=AD,
∴∠E=45°,∠EAD=90°,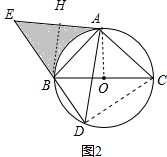
∴∠EAB=60°,
在Rt△HAB中,∵∠HAD=60°,
∴AH=
AB=1,BH=
AH=
,
在Rt△BHE中,∵∠E=45°,
∴EH=BH=
,
∴S△ABE=
×
×(1+
)=
,
∵∠AOB=2∠ACB=90°,
∴△AOB为等腰直角三角形,
∴OA=
AB=
,
∵S弓形AB=S扇形AOB-S△AOB=
-
×
×
=
π-1,
∴阴影部分的面积=
-(
π-1)=
.
 证明:∵AE=AD,
证明:∵AE=AD,∴∠E=∠ADE,
∵AB=AC,
∴∠ADE=∠ADC,
∴∠E=∠ADC,
∵∠ABE为圆内接四边形ABDC的外角,
∴∠ABE=∠ACD,
在△ABE和△ACD中,
|
△ABE≌△ACD,
∴BE=CD;
(2)连结OA、CD,作BH⊥AE于H,如图,
∵∠BAC=90°,AB=AC,
∴BC为直径,∠ABC=∠ACB=45°,
∴∠BDC=90°,
∵
 |
| BD |
| 1 |
| 2 |
 |
| CD |
∴∠DBC=2∠BCD,
∴∠DBC=60°,∠BCD=30°,
∴∠BAD=∠BCD=30°,
∵∠ADE=∠ACB=45°,
∵AE=AD,
∴∠E=45°,∠EAD=90°,

∴∠EAB=60°,
在Rt△HAB中,∵∠HAD=60°,
∴AH=
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△BHE中,∵∠E=45°,
∴EH=BH=
| 3 |
∴S△ABE=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
∵∠AOB=2∠ACB=90°,
∴△AOB为等腰直角三角形,
∴OA=
| ||
| 2 |
| 2 |
∵S弓形AB=S扇形AOB-S△AOB=
90•π•(
| ||
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
∴阴影部分的面积=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了全等三角形的判定与性质、扇形的面积公式.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
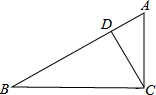 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,∠AOB等于∠COD,请判断∠AOC和∠BOD的大小关系并说明理由.
如图,∠AOB等于∠COD,请判断∠AOC和∠BOD的大小关系并说明理由.
 如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC. 如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,求线段FC的长.
如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,求线段FC的长.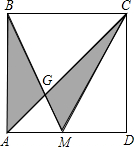 如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积.
如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积. 如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=
如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB= 如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数.
如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数.