题目内容
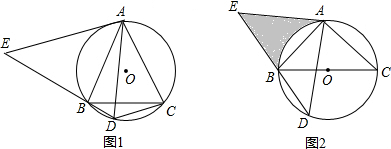
 如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.(1)求证:△OAE≌△OCF;
(2)求证:FC=OF;
(3)若BC=2
| 3 |
考点:矩形的性质,全等三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)欲证明△OAE≌△OCF,只要证明∠BAC=∠FCO,然后运用AAS公理即可解决问题.
(2)欲证明OF=CF,只要证明∠FOC=∠FCO;而∠BAC=∠FCO,∠AOE=∠FOC,故只需证明∠EAC=∠AOE即可解决问题.
(3)如图,作辅助线;首先证明AO=BO,EF⊥BO;进而证明2∠BAC+∠BAC=90°,得到∠BAC=30°,运用直角三角形的性质即可解决问题.
(2)欲证明OF=CF,只要证明∠FOC=∠FCO;而∠BAC=∠FCO,∠AOE=∠FOC,故只需证明∠EAC=∠AOE即可解决问题.
(3)如图,作辅助线;首先证明AO=BO,EF⊥BO;进而证明2∠BAC+∠BAC=90°,得到∠BAC=30°,运用直角三角形的性质即可解决问题.
解答: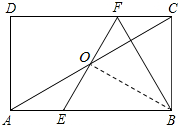 (1)证明:∵ABCD是矩形,
(1)证明:∵ABCD是矩形,
∴AB∥CD,
∴∠BAC=∠FCO,
在△AOE和△COF中,
,
∴△OAE≌△OCF(AAS),
(2)证明:∵∠BEF=2∠BAC,
且∠BEF=∠BAC+∠AOE,
∴∠BAC=∠AOE;
而∠BAC=∠FCO,∠AOE=∠FOC,
∴∠FCO=∠FOC,
∴FC=OF.
(2)解:如图,连接OB,
∵△OAE≌△OCF,
∴AO=CO,OE=OF;
∵BE=BF,OE=OF,
∴BO⊥EF,
∴∠BEF+∠ABO=90°,
∵∠ABC=90°,AO=CO,
∴AO=BO=
AC
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∵BC=3,
∴AC=2BC=6.
 (1)证明:∵ABCD是矩形,
(1)证明:∵ABCD是矩形,∴AB∥CD,
∴∠BAC=∠FCO,
在△AOE和△COF中,
|
∴△OAE≌△OCF(AAS),
(2)证明:∵∠BEF=2∠BAC,
且∠BEF=∠BAC+∠AOE,
∴∠BAC=∠AOE;
而∠BAC=∠FCO,∠AOE=∠FOC,
∴∠FCO=∠FOC,
∴FC=OF.
(2)解:如图,连接OB,
∵△OAE≌△OCF,
∴AO=CO,OE=OF;
∵BE=BF,OE=OF,
∴BO⊥EF,
∴∠BEF+∠ABO=90°,
∵∠ABC=90°,AO=CO,
∴AO=BO=
| 1 |
| 2 |
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∵BC=3,
∴AC=2BC=6.
点评:本题考查了矩形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,直角三角形30°角所对的直角边等于斜边的一半,综合题,但难度不大;(2)作辅助线并求出∠BAC=30°是解题的关键.

练习册系列答案
相关题目
在下列现象中,属于平移的是( )
| A、冰化为水 |
| B、电梯由一楼升到八楼 |
| C、导弹击中目标后爆炸 |
| D、卫星绕地球运动 |
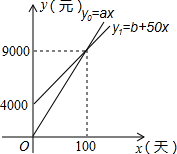 国家推行“节能减排,低碳经济”的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元.据市场调查知:每辆车改装前、后的燃料费(含改装费)(单位:元)与正常运营时间x(单位:天)之间分别满足关系式:y0=ax,y1=b+59x,其图象如图所示.根据图象解决下列问题:
国家推行“节能减排,低碳经济”的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元.据市场调查知:每辆车改装前、后的燃料费(含改装费)(单位:元)与正常运营时间x(单位:天)之间分别满足关系式:y0=ax,y1=b+59x,其图象如图所示.根据图象解决下列问题: 如图,六边形ABCDEF的每个内角都是120°,且AF=AB=3,BC=CD=2,求DE与EF的长.
如图,六边形ABCDEF的每个内角都是120°,且AF=AB=3,BC=CD=2,求DE与EF的长.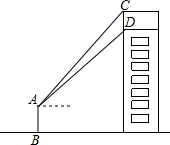 如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)
如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)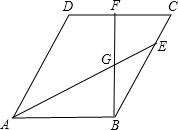 如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB
如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB
 如图,线段AD、BC相交于点E,AB⊥BC,BC⊥DC,BE=120,EC=60,DC=50,求AB的长.
如图,线段AD、BC相交于点E,AB⊥BC,BC⊥DC,BE=120,EC=60,DC=50,求AB的长.