题目内容
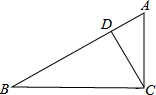 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:锐角三角函数的定义
专题:
分析:证明∠ACD=∠B,则∠ACD的余弦值等于∠B的余弦值,在直角△ABC中,利用勾股定理求得AB的长,利用余弦的定义求解.
解答:解:在直角△ABC中,AB=
=
=5.
∵在Rt△ABC中,∠C=90°,CD⊥AB于D.
∴∠ACD=∠B,
∴cosα=cosB=
=
.
故选A.
| AC2+BC2 |
| 32+42 |
∵在Rt△ABC中,∠C=90°,CD⊥AB于D.
∴∠ACD=∠B,
∴cosα=cosB=
| BC |
| AB |
| 4 |
| 5 |
故选A.
点评:本题考查了三角函数的求值,正确理解三角函数的性质:三角函数值值的大小是由角的大小确定,是解决本题的关键.

练习册系列答案
相关题目
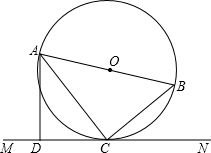 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC,CD=6,cos∠ACD=
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC,CD=6,cos∠ACD=| 3 |
| 5 |
| A、6.5 | B、6.25 |
| C、12.5 | D、12.25 |
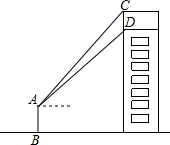 如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)
如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618) 已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗?
已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗?
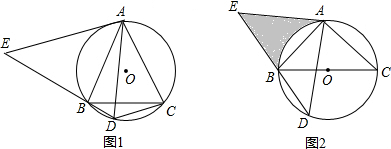
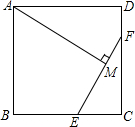 已知:E,F分别是正方形ABCD的边BC,CD上的点,AM⊥EF,垂足为M,AM=AB,
已知:E,F分别是正方形ABCD的边BC,CD上的点,AM⊥EF,垂足为M,AM=AB, 如图.菱形ABCD中.点E为AC上一点,且DE⊥BE.
如图.菱形ABCD中.点E为AC上一点,且DE⊥BE. 如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.