题目内容
5.已知动点P以每秒2cm的速度沿如图甲所示的边框按从B-C-D-E-F-A的路径移动,相应的△ABP的面积S与关于时间t的图象如图乙所示,若AB=6cm,求:(1)BC长为多少cm?
(2)图乙中a为多少cm2?
(3)图甲的面积为多少cm2?
(4)图乙中b为多少s?
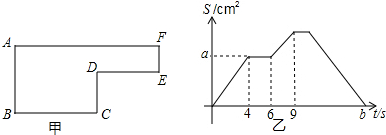
分析 (1)根据动点P以每秒2cm的速度,从B到C用的时间为4s,可以求得BC的长度;
(2)根据三角形的面积等于底乘以高除以2,可以得到a的值;
(3)根据题意和图形可以得到AB、AF的长,CD、DE的长,从而可以求得图甲的面积;
(4)根据题意和图形可以得到BC、CD、DE、EF、FA的长,从而可以得到b的值.
解答 解:(1)由图象可得,
点P从点B到点C运动的时间是4s,运动的速度是每秒2cm,
故BC的长度是:4×2=8cm,
即BC长是8cm;
(2)∵BC=8cm,AB=6cm,
∴S=$\frac{BC•AB}{2}=\frac{8×6}{2}=24c{m}^{2}$,
即图乙中a的值为24cm2;
(3)由图可知,
BC=4×2=8cm,CD=(6-4)×2=4cm,DE=(9-6)×2=6cm,AB=6cm,
∴AF=BC+DE=14cm,
∴图甲的面积是:AB•AF-CD•DE=6×14-4×6=84-24=60cm2;
(4)由题意可得,
b=$\frac{BC+CD+DE+EF+FA}{2}$=$\frac{8+4+6+(6-4)+(6+8)}{2}=17$s,
即b的值是17s.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
11.若关于x的二次三项式x2-ax+36是一个完全平方式,那么a的值是( )
| A. | 12 | B. | ±12 | C. | 6 | D. | ±6 |

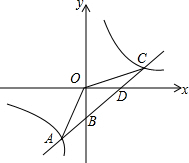 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.